题目内容
已知直线l过圆(x+4)2+y2=16的圆心C且垂直与x轴,点F的坐标是(-6,0),点G是圆上任意一点.
(1)若直线FG与直线l相交 于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(2)过点F人作两条互相垂直的弦,设其弦长为m.n,求m+n的最大值;
(3)在平面上是否存在定点P,使得对圆C上任意的点G,都有|GP|=2|GF|?若存在,求出点P的坐标;若存在,请说明理由.
(1)若直线FG与直线l相交 于点T,且G为线段FT的中点,求直线FG被圆C所截得的弦长;
(2)过点F人作两条互相垂直的弦,设其弦长为m.n,求m+n的最大值;
(3)在平面上是否存在定点P,使得对圆C上任意的点G,都有|GP|=2|GF|?若存在,求出点P的坐标;若存在,请说明理由.
考点:直线与圆相交的性质
专题:不等式的解法及应用,直线与圆
分析:(1)根据题意,求出直线FG的方程,圆心C到直线FG的距离d,利用勾股定理求出FG被圆C所截得的弦长;
(2)设两条弦的弦心距为d1,d2,则d12+d22=4,利用基本不等式求出m+n的最大值;
(3)假设存在定点P(s,t)满足题意,由|GP|=2|GF|点P的坐标,即可得出结论.
(2)设两条弦的弦心距为d1,d2,则d12+d22=4,利用基本不等式求出m+n的最大值;
(3)假设存在定点P(s,t)满足题意,由|GP|=2|GF|点P的坐标,即可得出结论.
解答:
解:(1)∵圆心C(-4,0),直线l:x=-4,F(-6,0),
根据题意设G(-5,y0),代入(x+4)2+y2=16,
解得y0=±
,∴kFG=±
;
∴直线FG的方程为y=±
(x+6),
∴点C(-4,0)到直线FG的距离为d=
,
直线FG被圆C所截得的弦长为2
=7;
(2)设两条弦的弦心距分别为d1,d2,则d12+d22=4;
∴m+n=2(
+
)≤2×2
=4
,
当且仅当d1=d2=
时取“=”,∴m+n的最大值是4
;
(3)假设存在定点P(s,t),设G(x0,y0),
则
=2
,
整理得3(x02+y02)+(48+2s)x0+2ty0+144-s2-t2=0;…①
又点G在圆C上,∴(x0+4)2+y02=16,即x02+y02=-8x0;…②
把②代入①,整理得(2s+24)x0+2ty0+144-s2-t2=0,
此时对圆上任意一点G(x0,y0)都成立,
∴
,解得
;
∴存在定点P(-12,0),使得对圆C上的任一点G都有|GP|=2|GF|.
根据题意设G(-5,y0),代入(x+4)2+y2=16,
解得y0=±
| 15 |
| 15 |
∴直线FG的方程为y=±
| 15 |
∴点C(-4,0)到直线FG的距离为d=
| ||
| 2 |
直线FG被圆C所截得的弦长为2
16-(
|
(2)设两条弦的弦心距分别为d1,d2,则d12+d22=4;
∴m+n=2(
| 16-d12 |
| 16-d22 |
|
| 14 |
当且仅当d1=d2=
| 2 |
| 14 |
(3)假设存在定点P(s,t),设G(x0,y0),
则
| (x0-s)2+(y0-t)2 |
| (x0+6)2+y02 |
整理得3(x02+y02)+(48+2s)x0+2ty0+144-s2-t2=0;…①
又点G在圆C上,∴(x0+4)2+y02=16,即x02+y02=-8x0;…②
把②代入①,整理得(2s+24)x0+2ty0+144-s2-t2=0,
此时对圆上任意一点G(x0,y0)都成立,
∴
|
|
∴存在定点P(-12,0),使得对圆C上的任一点G都有|GP|=2|GF|.
点评:本题考查了直线与圆的应用问题,也考查了基本不等式的应用问题,求直线被圆截得弦长的问题,是难题.

练习册系列答案
相关题目
已知函数f(x)=1+x-
+
-
+…+
(x>0),则f(x)在定义域上的单调性是( )
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2015 |
| 2015 |
| A、在(0,+∞)单调递增 |
| B、在(0,+∞)单调递减 |
| C、在(0,1)单调递增,在(1,+∞)单调递减 |
| D、在(0,1)单调递减,(1,+∞)单调递增 |
 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于A,B两点,交其准线于点C,若|
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于A,B两点,交其准线于点C,若|




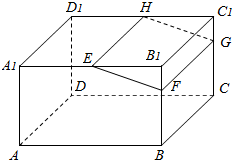 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.求证:FG∥平面ADD1A1.
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.求证:FG∥平面ADD1A1. 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<