题目内容
已知f(x)为奇函数,当x≥0时,f(x)=
,则不等式f(x)≤
解集为( )
|
| 1 |
| 2 |
A、[-
| ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[-
|
考点:分段函数的应用
专题:计算题,作图题,函数的性质及应用
分析:由题意作图,解出f(x)=
与f(x)=-
时的x的解集,从而求解不等式f(x)≤
解集.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
 解:作图如右图,
解:作图如右图,
当x>0时,令f(x)=
解得,x=
或x=
;
当x≥0时,令f(x)=-
解得,x=
;
则f(-
)=
;
则结合函数f(x)的图象可得,
x∈[-
,
]∪[
,+∞),
故选A.
 解:作图如右图,
解:作图如右图,当x>0时,令f(x)=
| 1 |
| 2 |
| 1 |
| 6 |
| ||
| 2 |
当x≥0时,令f(x)=-
| 1 |
| 2 |
| 2 |
则f(-
| 2 |
| 1 |
| 2 |
则结合函数f(x)的图象可得,
x∈[-
| 2 |
| 1 |
| 6 |
| ||
| 2 |
故选A.
点评:本题考查了学生的作图能力及数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=1+x-
+
-
+…+
(x>0),则f(x)在定义域上的单调性是( )
| x2 |
| 2 |
| x3 |
| 3 |
| x4 |
| 4 |
| x2015 |
| 2015 |
| A、在(0,+∞)单调递增 |
| B、在(0,+∞)单调递减 |
| C、在(0,1)单调递增,在(1,+∞)单调递减 |
| D、在(0,1)单调递减,(1,+∞)单调递增 |
 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于A,B两点,交其准线于点C,若|
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于A,B两点,交其准线于点C,若|




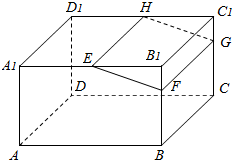 如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.求证:FG∥平面ADD1A1.
如图,在长方体ABCD-A1B1C1D1中,E、H分别是棱A1B1、D1C1上的点,且EH∥A1D1,过EH的平面与棱BB1、CC1相交,交点分别为F、G.求证:FG∥平面ADD1A1. 如图,平面内有三个向量
如图,平面内有三个向量