题目内容
在△ABC中，已知D是AB边上一点，若
=2
，
=λ
+μ
，则λ-μ= ．
| AD |
| DB |
| CD |
| CA |
| CB |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由于
=2
，可得
-
=2(
-
)，化为
=
+
．与
=λ
+μ
比较即可得出．
| AD |
| DB |
| CD |
| AD |
| CB |
| CD |
| CD |
| 1 |
| 3 |
| CA |
| 2 |
| 3 |
| CB |
| CD |
| CA |
| CB |
解答：
解：如图所示，
∵
=2
，
∴
-
=2(
-
)，
化为
=
+
．
∵
=λ
+μ
，
∴λ=
，μ=
，
∴λ-μ=-
．
故答案为：-
．
∵
| AD |
| DB |
∴
| CD |
| AD |
| CB |
| CD |
化为
| CD |
| 1 |
| 3 |
| CA |
| 2 |
| 3 |
| CB |
∵
| CD |
| CA |
| CB |
∴λ=
| 1 |
| 3 |
| 2 |
| 3 |
∴λ-μ=-
| 1 |
| 3 |
故答案为：-
| 1 |
| 3 |
点评：本题考查了向量的三角形法则、向量相等，属于基础题．
练习册系列答案
相关题目
如图，⊙O是△ABC的外接圆，AB=AC，延长BC到点D，使得CD=AC，连结AD交⊙O于点E，连结BE，若∠D=35°，则∠ABE的大小为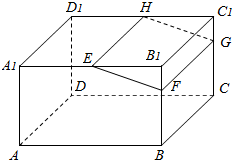
如图，在长方体ABCD-A1B1C1D1中，E、H分别是棱A1B1、D1C1上的点，且EH∥A1D1，过EH的平面与棱BB1、CC1相交，交点分别为F、G．求证：FG∥平面ADD1A1．已知0≤x≤π，且-
＜a＜0，那么函数f（x）=cos2x-2asinx-1的最小值是（ ）
| 1 |
| 2 |
| A、2a+1 | B、2a-1 |
| C、-2a-1 | D、2a |