Question

15．已知正方体ABCD-A₁B₁C₁D₁的棱长为4，点E、F、G、H分别在棱CC₁、DD₁、BB₁、BC上，且CE=$\frac{1}{2}$CC₁，DF=BG=$\frac{1}{4}$DD₁，BH=$\frac{1}{2}$BC，求AH与平面AFEG的夹角．

Answer 1

分析 以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能求出AH与平面AFEG的夹角．

解答 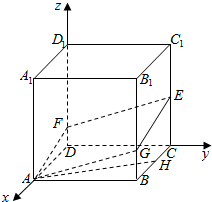解：以D为原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，
∵点E、F、G、H分别在棱CC₁、DD₁、BB₁、BC上，且CE=$\frac{1}{2}$CC₁，DF=BG=$\frac{1}{4}$DD₁，BH=$\frac{1}{2}$BC，
∴A（4，0，0），H（2，4，0），F（0，0，1），G（4，4，1），
$\overrightarrow{AH}$=（-2，4，0），$\overrightarrow{AF}$=（-4，0，1），$\overrightarrow{AG}$=（0，4，1），
设平面AFEG的法向量$\overrightarrow{n}$=（x，y，z），
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AF}=-4x+z=0}\\{\overrightarrow{n}•\overrightarrow{AG}=4y+z=0}\end{array}\right.$，取x=1，得$\overrightarrow{n}$=（1，-1，4），
设AH与平面AFEG的夹角为θ，
则sinθ=$\frac{|\overrightarrow{AH}•\overrightarrow{n}|}{|\overrightarrow{AH}|•|\overrightarrow{n}|}$=$\frac{|-2-4|}{\sqrt{20}•\sqrt{18}}$=$\frac{\sqrt{10}}{10}$．
∴$θ=arcsin\frac{\sqrt{10}}{10}$．
∴AH与平面AFEG的夹角为arcsin$\frac{\sqrt{10}}{10}$．

点评 本题考查线面角的求法，是中档题，解题时要认真审题，注意向量法的合理运用．