题目内容
3.已知f(x)=x5+ax3+bx-10,且f(-3)=10,则f(3)=-30.分析 函数f(x)不具备奇偶性,但其中g(x)=x5+ax3+bx是奇函数,则可充分利用奇函数的定义解决问题.
解答 解:令g(x)=x5+ax3+bx,由函数奇偶性的定义,易得其为奇函数;
则f(x)=g(x)-10
所以f(-3)=g(-3)-10=10
得g(-3)=20,又因为g(x)是奇函数,即g(3)=-g(-3)
所以g(3)=-20,则f(3)=g(3)-10=-30.
故答案为:-30.
点评 本题较灵活地考查奇函数的定义.

练习册系列答案
相关题目
8.函数f(x)=2x-x2的零点的个数为( )
| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
12.下列结论:①函数y=x(1-3x)(x>0)有最大值$\frac{1}{12}$;②函数y=2-4x-$\frac{4}{x}$(x<0)有最大值10;③若a<0,则(1+a)(1+$\frac{1}{a}$)≥4.正确的序号是( )
| A. | ① | B. | ①③ | C. | ②③ | D. | ①②③ |
13.集合A={x|-2-a<x<a,a>0},命题p:1∈A,命题q:2∈A,若p∨q为真命题,p∧q为假命题,则a的取值范围是( )
| A. | 0<a<1或a>2 | B. | 0<a<1或α≥2 | C. | 1<a≤2 | D. | 1≤a≤2 |
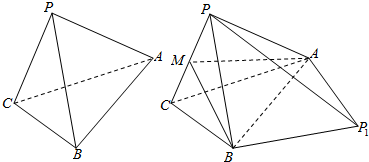 如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.
如图1,四面体PABC中,BC=BP=1,AC=AP=$\sqrt{3}$,AB=2,将△PAB沿直线AB翻折至△P1AB,使点A,P1,B,C在同一平面内(如图2),点M为PC中点.