题目内容
有一块半径为R,圆心角为60°(∠AOB=60°)的扇形木板,现欲按如图所示锯出一矩形(矩形EFGN)桌面,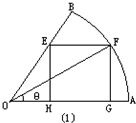 则此桌面的最大面积为 .
则此桌面的最大面积为 .
 则此桌面的最大面积为
则此桌面的最大面积为考点:三角函数的最值,弧度制
专题:三角函数的求值
分析:求最大值问题这里应构造函数,利用三角函数的有界性求解三角函数的最值.
解答:
解:如图设∠FOA=θ,则FG=Rsinθ,
在△OEF中,EF=
.
又设矩形EFGH的面积为S,那么S=FG•EF=
=
[cos(2θ-60°)-
]
又∵0°<θ<60°,故当cos(2θ-60°)=1,即θ=30°时,S取最大值
(1-
)=
故答案为:
.

在△OEF中,EF=
| 2Rsin(60°-θ) | ||
|
又设矩形EFGH的面积为S,那么S=FG•EF=
| 2R2sin(60°-θ)sinθ | ||
|
=
| R2 | ||
|
| 1 |
| 2 |
又∵0°<θ<60°,故当cos(2θ-60°)=1,即θ=30°时,S取最大值
| R2 | ||
|
| 1 |
| 2 |
| ||
| 6 |
故答案为:
| ||
| 6 |
点评:本题关键是如何利用角θ表示矩形的长与宽,合理地把长与宽放在三角形中,考查三角函数的最值的求法..

练习册系列答案
相关题目
已知等差数列{an},满足a2=3,a3=2,则公差d=( )
| A、-1 | B、1 | C、-2 | D、2 |