题目内容
已知两个不重合的平面α、β及三条不重合的直线m、n、l.给出下列命题:
①当m?α,且n?α时,若n∥α,则m∥n;
②当α⊥β,α∩β=m,n⊥β时,若n⊥m,则n⊥α;
③当m?α时,若m⊥β,则α⊥β;
④当m⊥α,n⊥β时,若m∥n,则α∥β
则逆命题成立的个数是( )
①当m?α,且n?α时,若n∥α,则m∥n;
②当α⊥β,α∩β=m,n⊥β时,若n⊥m,则n⊥α;
③当m?α时,若m⊥β,则α⊥β;
④当m⊥α,n⊥β时,若m∥n,则α∥β
则逆命题成立的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:由直线与平面平行的判定定理①的逆命题成立;②的逆命题不存在;由m与β相交、平行或m?β,知③的逆命题不成立;由直线与平面平行的性质定理知m∥n,知④的逆命题成立.
解答:
解:当m?α,且n?α时,
若m∥n,则由直线与平面平行的判定定理知n∥α,故①的逆命题成立;
当α⊥β,α∩β=m,n⊥β时,n∥α或n?α,故②的逆命题不存在;
当m?α时,若α⊥β,则m与β相交、平行或m?β,故③的逆命题不成立;
当m⊥α,n⊥β时,若α∥β,
则由直线与平面平行的性质定理知m∥n,故④的逆命题成立.
故选:B.
若m∥n,则由直线与平面平行的判定定理知n∥α,故①的逆命题成立;
当α⊥β,α∩β=m,n⊥β时,n∥α或n?α,故②的逆命题不存在;
当m?α时,若α⊥β,则m与β相交、平行或m?β,故③的逆命题不成立;
当m⊥α,n⊥β时,若α∥β,
则由直线与平面平行的性质定理知m∥n,故④的逆命题成立.
故选:B.
点评:本题考查命题真假的判断,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
已知函数f(x)=
,则不等式f(3-x2)<f(2x)的解集为( )
|
| A、(-3,1) | ||||
B、[-
| ||||
C、[
| ||||
D、(
|
已知函数f(x)=
,若函数y=f2(x)-2bf(x)+b-
有6个零点,则b的取值范围是( )
|
| 2 |
| 9 |
A、[
| ||||||||
B、(
| ||||||||
C、(0,
| ||||||||
D、(
|
要得到函数y=cos2x的图象,只需将y=sin(2x+
)的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知中心在坐标原点的双曲线C与抛物线x2=2px(p>0)有相同的焦点F,点A是两曲线的交点,且AF⊥y轴,则双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列函数中,既是奇函数又在(0,+∞)单调递增的函数是( )
| A、y=x3 |
| B、y=ex |
| C、y=x-1 |
| D、y=lnx |
已知全集U={1,2,3,4,5,6,7},A={2,4,6},B={1,3,5,7},则A∩(∁UB)等于( )
| A、{2,4,6} |
| B、{1,3,5} |
| C、{2,4,5} |
| D、{2,5} |
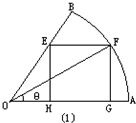 则此桌面的最大面积为
则此桌面的最大面积为