题目内容
函数y=sin(x+
)的单调递减区间是 .
| π |
| 4 |
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:令2kπ+
≤x+
≤2kπ+
,k∈z,求得x的范围,可得函数的单调递减区间.
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
解答:
解:令2kπ+
≤x+
≤2kπ+
,k∈z,求得 2kπ+
≤x≤
+2kπ,
故函数y=sin(x+
)的单调递减区间是[2kπ+
,
+2kπ],k∈z,
故答案为:[2kπ+
,
+2kπ],k∈z.
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
故函数y=sin(x+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
故答案为:[2kπ+
| π |
| 4 |
| 5π |
| 4 |
点评:本题主要考查正弦函数的减区间,属于基础题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
已知(1-2x)n展开式中,二项式系数之和为128,则(1-2x)n(1+x)展开式中含x2项的系数为( )
| A、71 | B、70 | C、21 | D、49 |
已知中心在坐标原点的双曲线C与抛物线x2=2px(p>0)有相同的焦点F,点A是两曲线的交点,且AF⊥y轴,则双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
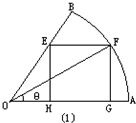 则此桌面的最大面积为
则此桌面的最大面积为