题目内容
已知等差数列{an},满足a2=3,a3=2,则公差d=( )
| A、-1 | B、1 | C、-2 | D、2 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:利用等差数列的通项公式求解.
解答:
解:∵等差数列{an},满足a2=3,a3=2,
∴公差d=a3-a2=2-3=-1.
故选:A.
∴公差d=a3-a2=2-3=-1.
故选:A.
点评:本题考查等差数列的公差的求法,是基础题,解题时要注意等差数列的公差的合理运用.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
已知(1-2x)n展开式中,二项式系数之和为128,则(1-2x)n(1+x)展开式中含x2项的系数为( )
| A、71 | B、70 | C、21 | D、49 |
在区间(0,1)中随机地取出两个数,则两数之和小于
的概率是( )
| 5 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
| D、以上都不对 |
已知函数f(x)=
,则不等式f(3-x2)<f(2x)的解集为( )
|
| A、(-3,1) | ||||
B、[-
| ||||
C、[
| ||||
D、(
|
下列函数中,既是奇函数又在(0,+∞)单调递增的函数是( )
| A、y=x3 |
| B、y=ex |
| C、y=x-1 |
| D、y=lnx |
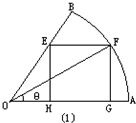 则此桌面的最大面积为
则此桌面的最大面积为