题目内容
△ABC中，|
|cos∠ACB=|
|cos∠CAB=
，且
•
=0，则AB长为 ．
| CB |
| BA |
| 3 |
| AB |
| BC |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：先由两向量数量积为0，根据数量积的定义得出∠ABC=90°，为了用上|
|cos∠ACB=|
|cos∠CAB=
，计算
•
和
•
，下面就要看经计算得到什么，以及能否用得出的结果求出AB的长．
| CB |
| BA |
| 3 |
| CB |
| CA |
| AB |
| AC |
解答：
解：由
•
=0得：∠ABC=90°；
•
=|
|•|
|cos∠ACB=
|
|，
.
=|
|•|
=
|
∴
•
=
•
，即：
•
-
•
=0，∴
•(
+
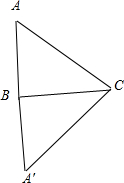
)=0，如右图，A′是延长AB所得，且AB=BA′，则CA=CA′，
=
，所以
+
=
；
•
=0，所以∠ACA′=90°，∴∠CAB=45°，则∠cos45°=
；
所以|
|=
，即AB长为
．
解：由| AB |
| BC |
| CB |
| CA |
| CB |
| CA |
| 3 |
| CA |
| AB |
| AC |
| AB |
| AC|cos∠BAC |
| 3 |
| AC| |
∴
| CB |
| CA |
| AB |
| AC |
| CB |
| CA |
| AB |
| AC |
| CA |
| CB |
| AB |
| AB |
| BA′ |
| CB |
| AB |
| CA′ |
| CA |
| CA′ |
| ||
| 2 |
所以|
| AB |
| 6 |
| 6 |
点评：本题考查你如何利用上条件，本题是构造了两个向量的数量积，这一点对解决这道题很关键，本题用到了向量数量积的计算公式和向量的加法运算．
练习册系列答案
相关题目