Question

已知a，b是实数，函数f（x）=ax+b丨x-1丨（x∈R）
（1）若a，b∈（-2，2），且函数f（x）在（0，+∞）内存在最大值，试在平面直角坐标系aOb中求出动点（a，b）运动区域的面积；
（2）若b＞0，且关于x的不等式f（x）＜0的解集中的整数恰巧有两个，试求

a

b

的取值范围．

Answer 1

考点：函数的最值及其几何意义

专题：综合题,函数的性质及应用

分析：（1）先化简函数，若a，b∈（-2，2），且函数f（x）在（0，+∞）内存在最大值，则需

a+b＜0 a-b＞0 -2＜a＜2 -2＜b＜2

，利用区域，即可求出区域的面积；
（2）由题意，需

f(2)＜0 f(3)≥0

，即可得出结论．

解答： 解：（1）f（x）=

(a+b)x-b，x≥1 (a-b)x+b，x＜1

．
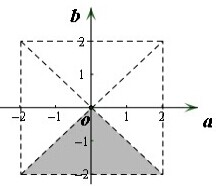
若a，b∈（-2，2），且函数f（x）在（0，+∞）内存在最大值，则需

a+b＜0 a-b＞0 -2＜a＜2 -2＜b＜2

，
如图所示，∴动点（a，b）运动区域的面积S=

1

2

×4×2=4；
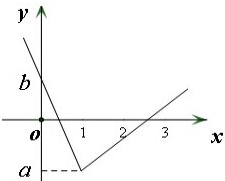
（2）b＞0，且关于x的不等式f（x）＜0的解集中的整数恰巧有两个，
则需

f(2)＜0 f(3)≥0

，即

2a+b＜0 3a+2b≥0

，解得-

2

3

≤

a

b

＜-

1

2

．

点评：本题考查函数的最值及其几何意义，考查数形结合的数学思想，考查学生分析解决问题的能力，属于中档题．