题目内容
已知定义在R上的函数f(x)满足:f(x+2)=f(x+1)-f(x),若f(2)=-lg2,f(3)=-lg5,则f(2014)= .
考点:抽象函数及其应用,对数的运算性质
专题:函数的性质及应用
分析:利用题中条件:“f(x+2)=f(x+1)-f(x)”得出函数f(x)是周期函数,从而求出f(2014)即可
解答:
解:∵f(x+2)=f(x+1)-f(x),
∴f(x+3)=f(x+2)-f(x+1)=f(x+1)-f(x)-f(x+1)=-f(x),
∴f(x+6)=-f(x+3)=f(x),
∴f(x)是周期为6的周期函数,
∴f(2014)=f(335×6+4)=f(4)=f(3)-f(2)=-lg5+lg2=-lg
+lg2=-(1-lg2)+lg2=-1+lg4,
故答案为:-1+lg4
∴f(x+3)=f(x+2)-f(x+1)=f(x+1)-f(x)-f(x+1)=-f(x),
∴f(x+6)=-f(x+3)=f(x),
∴f(x)是周期为6的周期函数,
∴f(2014)=f(335×6+4)=f(4)=f(3)-f(2)=-lg5+lg2=-lg
| 10 |
| 2 |
故答案为:-1+lg4
点评:本题主要考查了抽象函数及其应用,考查分析问题和解决问题的能力,属于中档题

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
用二分法求方程3x+3x-8=0在区间(1,2)的过程中,设函数f(x)=3x+3x-8,算得f(1)<0,f(1.25)<0,f(1.5)>0,f(1.75)>0,则该方程的根属于( )
| A、(1,1.25) |
| B、(1.25,1.5) |
| C、(1.5,1.75) |
| D、(1.75,2) |
 如图,直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点,F是A1C上的点.
如图,直三棱柱ABC-A1B1C1的底面ABC是等腰直角三角形,AB=AC=1,侧棱AA1⊥底面ABC,且AA1=2,E是BC的中点,F是A1C上的点.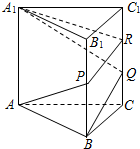 已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等.蚂蚁甲从A点沿表面经过棱BB1,CC1爬到点A1,蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图,设∠PAB=α,∠QBC=β,若两只蚂蚁各自爬过的路程最短,则α+β=
已知正三棱柱ABC-A1B1C1的底面边长与侧棱长相等.蚂蚁甲从A点沿表面经过棱BB1,CC1爬到点A1,蚂蚁乙从B点沿表面经过棱CC1爬到点A1.如图,设∠PAB=α,∠QBC=β,若两只蚂蚁各自爬过的路程最短,则α+β=