题目内容
某几何体的三视图如图所示，则该几何体的表面积等于（ ）| A、64 | B、92 | C、78 | D、56 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图知几何体为一四棱柱，且四棱柱的高为4，底面为直角梯形，直角梯形的直角腰为4，两底边长分别为2，5，求得另一腰长，把数据代入表面积公式计算．
解答：
解：由三视图知几何体为一四棱柱，且四棱柱的高为4，
底面为直角梯形，直角梯形的直角腰为4，两底边长分别为2，5，另一腰长为
=5；
∴几何体的表面积S=S底面+S侧面=2×
×4+（2+4+5+5）×4=92．
故选B．
底面为直角梯形，直角梯形的直角腰为4，两底边长分别为2，5，另一腰长为
| 42+32 |
∴几何体的表面积S=S底面+S侧面=2×
| 2+5 |
| 2 |
故选B．
点评：本题考查了由三视图求几何体的表面积，由三视图判断几何体的形状及数据所对应的几何量是解题的关键．
练习册系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知A、B、C是单位圆上三个互不相同的点．若|
|=|
|，则
•
的最小值是（ ）
| AB |
| AC |
| AB |
| AC |
| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
记等差数列{an}的前n项和为Sn，已知S7=28，S8=36，则S15=（ ）
| A、210 | B、120 |
| C、64 | D、56 |
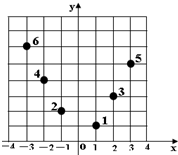如图，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横纵坐标分别对应数列{an}（n∈N*）的前12项，如下表所示：| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A、501 | B、502 |
| C、503 | D、504 |
在△ABC中，AB=1，BC=2，
•
=
，则角B=（ ）
| BA |
| BC |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |