题目内容
已知A、B、C是单位圆上三个互不相同的点.若|
|=|
|,则
•
的最小值是( )
| AB |
| AC |
| AB |
| AC |
| A、0 | ||
B、-
| ||
C、-
| ||
D、-
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由题意可得,点A在BC的垂直平分线上,不妨设单位圆的圆心为O(0,0),点A(0,1),点B(x1,y1),则点C(-x1,y1),x12+y12=1,且-1≤y1<1.根据
•
=2y12-2y1,再利用二次函数的性质求得它的最小值.
| AB |
| AC |
解答:
 解:由题意可得,点A在BC的垂直平分线上,不妨设单位圆
解:由题意可得,点A在BC的垂直平分线上,不妨设单位圆
的圆心为O(0,0),
点A(0,1),点B(x1,y1),则点C(-x1,y1),
-1≤y1<1.
∴
=(x1,y1-1),
=(-x1,y1-1),x12+y12=1.
∴
•
=-x12+y12-2y1+1=-(1-y12)+y12-2y1+1
=2y12-2y1,
∴当y1=
时,
•
取得最小值为-
,
故选:C.
 解:由题意可得,点A在BC的垂直平分线上,不妨设单位圆
解:由题意可得,点A在BC的垂直平分线上,不妨设单位圆的圆心为O(0,0),
点A(0,1),点B(x1,y1),则点C(-x1,y1),
-1≤y1<1.
∴
| AB |
| AC |
∴
| AB |
| AC |
=2y12-2y1,
∴当y1=
| 1 |
| 2 |
| AB |
| AC |
| 1 |
| 2 |
故选:C.
点评:本题主要考查两个向量的数量积公式,二次函数的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
随着科技发展计算机价格不断降低,每年计算机价格降低
,2000年价格为8100元的计算机,2004年价格可降为( )
| 1 |
| 3 |
| A、1800 | B、1600 |
| C、900 | D、300 |
已知向量
=(-1,2),
=(3,m),m∈R,则“m=-6”是“
∥(
+
)”的( )
| a |
| b |
| a |
| a |
| b |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
 某几何体的三视图如图所示,则该几何体的表面积等于( )
某几何体的三视图如图所示,则该几何体的表面积等于( )| A、64 | B、92 | C、78 | D、56 |
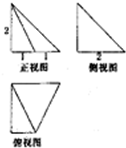 某几何体的三视图如图所示,则其侧面的直角三角形的个数为( )
某几何体的三视图如图所示,则其侧面的直角三角形的个数为( )| A、1 | B、2 | C、3 | D、4 |