题目内容
在△ABC中，AB=1，BC=2，
•
=
，则角B=（ ）
| BA |
| BC |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
考点：平面向量数量积的运算
专题：解三角形
分析：由题意利用两个向量的数量积的定义可得 1×2×cosB=
，解得cosB的值，可得B的值．
| 3 |
解答：
解：在△ABC中，∵AB=1，BC=2，
•
=
，
则 1×2×cosB=
，
解得cosB=
，
∴B=30°，
故选：A．
| BA |
| BC |
| 3 |
则 1×2×cosB=
| 3 |
解得cosB=
| ||
| 2 |
∴B=30°，
故选：A．
点评：本题主要考查两个向量的数量积的定义，属于基础题．
练习册系列答案
相关题目
随着科技发展计算机价格不断降低，每年计算机价格降低
，2000年价格为8100元的计算机，2004年价格可降为（ ）
| 1 |
| 3 |
| A、1800 | B、1600 |
| C、900 | D、300 |
某几何体的三视图如图所示，则该几何体的表面积等于（ ）| A、64 | B、92 | C、78 | D、56 |
等差数列{an}的公差d≠0，an∈R，前n项和为Sn，则对正整数m，下列四个结论中：
（1）Sm，S2m-Sm，S3m-S2m成等差数列，也可能成等比数列；
（2）Sm，S2m-Sm，S3m-S2m成等差数列，但不可能成等比数列；
（3）Sm，S2m，S3m可能成等比数列，但不可能成等差数列；
（4）Sm，S2m，S3m不可能成等比数列，也不可能成等差数列；
正确的是（ ）
（1）Sm，S2m-Sm，S3m-S2m成等差数列，也可能成等比数列；
（2）Sm，S2m-Sm，S3m-S2m成等差数列，但不可能成等比数列；
（3）Sm，S2m，S3m可能成等比数列，但不可能成等差数列；
（4）Sm，S2m，S3m不可能成等比数列，也不可能成等差数列；
正确的是（ ）
| A、（1）（3） |
| B、（1）（4） |
| C、（2）（3） |
| D、（2）（4） |
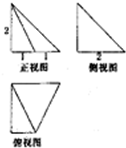某几何体的三视图如图所示，则其侧面的直角三角形的个数为（ ）| A、1 | B、2 | C、3 | D、4 |