题目内容
已知等差数列{an}的公差为-1,且a2+a7+a12=-6,
(1)求数列{an}的通项公式an与前n项和Sn;
(2)若{bn}是首项为4,公比为
的等比数列,前n项和为Tn,求证:当t>6时,对任意n,m∈N*,Sn<Tm+t恒成立.
(1)求数列{an}的通项公式an与前n项和Sn;
(2)若{bn}是首项为4,公比为
| 1 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据题设条件,利用等差数列通项公式求出公差,由此能求出数列{an}的通项公式an与前n项和Sn.
(2)由已知条件,利用等比数列前n项和公式求出Tn,分别求出Tn的最小值和Sn的最大值,由此能够证明当t>6时,对任意n,m∈N*,Sn<Tm+t恒成立.
(2)由已知条件,利用等比数列前n项和公式求出Tn,分别求出Tn的最小值和Sn的最大值,由此能够证明当t>6时,对任意n,m∈N*,Sn<Tm+t恒成立.
解答:
(本题满分14分)
解:(1)∵等差数列{an}的公差为-1,且a2+a7+a12=-6,
∴3a7=-6,解得a7=-2,
∵a7=a1+6(-1)=-2,解得a1=4,(3分)
∴an=a1+(n-1)d=5-n,(5分)
∴Sn=
=
.(7分)
(2)∵{bn}是首项为4,公比为
的等比数列,前n项和为Tn,
∴Tn=
=8[(1-(
)n],Tm≥T1=4,(9分)
又∵Sn=
=-
(n2-9n)=-
[(n-
)2-
],
∴(Sn)max=S4=S5=10,(11分)
当t>6时,对任意m,n∈N*,Tm+t>T1+6>10≥Sn,
∴当t>6时,对任意n,m∈N*,Sn<Tm+t恒成立.(14分)
解:(1)∵等差数列{an}的公差为-1,且a2+a7+a12=-6,
∴3a7=-6,解得a7=-2,
∵a7=a1+6(-1)=-2,解得a1=4,(3分)
∴an=a1+(n-1)d=5-n,(5分)
∴Sn=
| n(a1+an) |
| 2 |
| n(9-n) |
| 2 |
(2)∵{bn}是首项为4,公比为
| 1 |
| 2 |
∴Tn=
4[1-(
| ||
1-
|
| 1 |
| 2 |
又∵Sn=
| n(9-n) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
| 81 |
| 4 |
∴(Sn)max=S4=S5=10,(11分)
当t>6时,对任意m,n∈N*,Tm+t>T1+6>10≥Sn,
∴当t>6时,对任意n,m∈N*,Sn<Tm+t恒成立.(14分)
点评:本题考查数列的通项公式的求法,考查数列前n和的应用,是中档题,解题时要注意等价转化思想的合理运用.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 某几何体的三视图如图所示,则该几何体的表面积等于( )
某几何体的三视图如图所示,则该几何体的表面积等于( )| A、64 | B、92 | C、78 | D、56 |
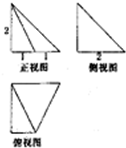 某几何体的三视图如图所示,则其侧面的直角三角形的个数为( )
某几何体的三视图如图所示,则其侧面的直角三角形的个数为( )| A、1 | B、2 | C、3 | D、4 |