题目内容
定义两个平面向量的一种新运算
?
=|
|•|
|sin＜
，
＞，（其中＜
，
＞表示
，
的夹角），则对于两个平面向量
，
，下列结论不一定成立的是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||||||||||
B、（
| ||||||||||||
C、λ（
| ||||||||||||
D、若
|
考点：进行简单的合情推理
专题：规律型,平面向量及应用
分析：根据平面向量的运算律及运算法则，结合新运算，分别进行判断即可．
解答：
解：A中，∵
?
=|
|•|
|sin＜
，
＞，
∴
?
=|
|•|
|sin＜
，
＞，
?
=
?
，故A正确；
B中，由
?
=|
|•|
|sin＜
，
＞，
•
=|
|•|
|cos＜
，
＞，
可知（
?
）2+（
•
）2=|
|2•|
|2，故B正确；
C中，λ（
?
）=λ|
|•|
|sin＜
，
＞，（λ
）?
=|λ
|•|
|sin＜
，
＞，
当λ＜0时，λ（
?
）=（λ
）?
不成立，故C错误；
∵
?
=|
|•|
|sin＜
，
＞=0，
则|
|=0，此时
=
，满足
∥
；
或|
|=0，此时
=
，满足
∥
；
或sin＜
，
＞=0此时＜
，
＞=
，满足
∥
；
综上，D正确；
故选：C．
| a |
| b |
| a |
| b |
| a |
| b |
∴
| b |
| a |
| a |
| b |
| a |
| b |
| a |
| b |
| b |
| a |
B中，由
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
可知（
| a |
| b |
| a |
| b |
| a |
| b |
C中，λ（
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
当λ＜0时，λ（
| a |
| b |
| a |
| b |
∵
| a |
| b |
| a |
| b |
| a |
| b |
则|
| a |
| a |
| 0 |
| a |
| b |
或|
| b |
| b |
| 0 |
| a |
| b |
或sin＜
| a |
| b |
| a |
| b |
| 0 |
| a |
| b |
综上，D正确；
故选：C．
点评：本题主要考查向量的基本运算，根据新定义结合向量的基本运算即可判断，比较基础．
练习册系列答案
课课练江苏系列答案
名牌中学课时作业系列答案
明天教育课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
定义在复数集上的函数f（z-i）=
，则f（i）=（ ）
| ||
| 1-z |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
在区间[0，2]和[1，2]上分别取一个数x，y，则对应的数对（x，y）是不等式x-y≤0的解的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
设函数f（x）=
，类比课本推导等差数列前n项和公式的推导方法计算f（-4）+f（-3）+…+f（0）+f（1）+…+f（4）+f（5）的值为（ ）
| 1 | ||
2x+
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若 13+23+33+…+n3=n2（an2+bn+c），n∈N*，则abc=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知各项均为正数的数列{an}满足a1=1，an+2an=39（n∈N*），那么数列{an}的前50项和S50的最小值为（ ）
| A、637 | ||
| B、559 | ||
C、481+25
| ||
D、492+24
|
函数f（x）=x3-ax在（-∞，1]上递增，则a的范围是（ ）
| A、a＞3 | B、a≥3 |
| C、a＜3 | D、a≤3 |
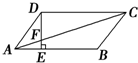如图所示，在平行四边形ABCD中，AE：EB=1：2，若S△AEF=6cm2，则S△ADF为（ ）| A、54cm2 |
| B、24cm2 |
| C、18cm2 |
| D、12cm2 |