题目内容
已知各项均为正数的数列{an}满足a1=1,an+2an=39(n∈N*),那么数列{an}的前50项和S50的最小值为( )
| A、637 | ||
| B、559 | ||
C、481+25
| ||
D、492+24
|
考点:数列的求和,基本不等式
专题:等差数列与等比数列
分析:由已知条件推导出a1=1,a3=39,a5=1,a7=39,…,a47=39,a49=1,a2a4=39,所以a2+a4≥2
,当且仅当a2=a4=
时取等号,故当偶数项都是
时,S50取最小值,由此能求出S50的最小值.
| 39 |
| 39 |
| 39 |
解答:
解:∵各项均为正数的数列{an}满足a1=1,an+2an=39(n∈N*),
∴a1=1,a3=39,a5=1,a7=39,…,a47=39,a49=1,
a2a4=39,∴a2+a4≥2
,当且仅当a2=a4=
时取等号,
∴当偶数项都是
时,S50取最小值,
∴(S50)min=12×(1+39)+1+25
=481+25
.
故选:C.
∴a1=1,a3=39,a5=1,a7=39,…,a47=39,a49=1,
a2a4=39,∴a2+a4≥2
| 39 |
| 39 |
∴当偶数项都是
| 39 |
∴(S50)min=12×(1+39)+1+25
| 39 |
| 39 |
故选:C.
点评:本题考查数列的前50项和的最小值的求法,是中档题,解题时节要认真审题,注意均值定理的合理运用.

练习册系列答案
相关题目
已知F是抛物线y=
x2的焦点,P是该抛物线上的动点,则PF中点的轨迹方程是( )
| 1 |
| 8 |
| A、x2-4y+2=0 |
| B、2x2-8y+1=0 |
| C、x2-4y+4=0 |
| D、2x2-8y+6=0 |
如图,A1B1C1-ABC是三棱柱,下列直线中与AA1成异面直线的是( )


| A、BB1 |
| B、CC1 |
| C、B1C1 |
| D、AB |
已知等差数列{an}中,a2=4,a6=12,则公差d等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
定义两个平面向量的一种新运算
?
=|
|•|
|sin<
,
>,(其中<
,
>表示
,
的夹角),则对于两个平面向量
,
,下列结论不一定成立的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||||||||||
B、(
| ||||||||||||
C、λ(
| ||||||||||||
D、若
|
如图所示,AT切⊙O于T,若AT=2
,AE=3,AD=4,DE=2,则BC等于( )

| 6 |

| A、3 | B、4 | C、6 | D、8 |
已知函数f(x)=x3+ax2-x+c(x∈R),下列结论错误的是( )
| A、函数f(x)一定存在极大值和极小值 | ||||
B、若函数f(x)在(-∞,x1),(x2,+∞)上是增函数,则x2-x1≥
| ||||
| C、函数f(x)的图象是中心对称图形 | ||||
| D、函数f(x)一定存在三个零点 |
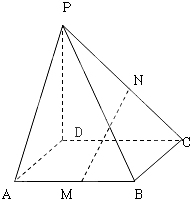 在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;
在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;