题目内容
已知f(x)=ax+
(a>1).用反证法证明方程f(x)=0没有负数根.
| x-2 |
| x+1 |
考点:反证法与放缩法
专题:证明题,反证法
分析:假设f(x)=0 有负根 x0,即 f(x0)=0,根据f(0)=-1,可得 f(x0)>f(0)①,若-1<x0<0,由条件可得f(x0)<f(0)=-1,这与①矛盾,若x0<-1,可得 f(x0)>0,这也与①矛盾.
解答:
证明:假设f(x)=0 有负根 x0,且 x0≠-1,即 f(x0)=0.
根据f(0)=-1,可得 f(x0)>f(0)①.
若-1<x0<0,由a>1,可知y=ax是增函数,y=
在(-1,+∞)是增函数,可知函数f(x)=ax+
在(-1,+∞)是增函数,可得f(x0)<f(0)=-1,这与①矛盾.
若x0<-1,则 ax0>0,x0-2<0,x0+1<0,∴f(x0)>0,这与题目条件矛盾.
故假设不正确.
∴方程ax+
=0 没有负根.
根据f(0)=-1,可得 f(x0)>f(0)①.
若-1<x0<0,由a>1,可知y=ax是增函数,y=
| x-2 |
| x+1 |
| x-2 |
| x+1 |
若x0<-1,则 ax0>0,x0-2<0,x0+1<0,∴f(x0)>0,这与题目条件矛盾.
故假设不正确.
∴方程ax+
| x-2 |
| x+1 |
点评:本题考查用反证法证明数学命题,推出矛盾,是解题的关键和难点.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
定义两个平面向量的一种新运算
?
=|
|•|
|sin<
,
>,(其中<
,
>表示
,
的夹角),则对于两个平面向量
,
,下列结论不一定成立的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||||||||||
B、(
| ||||||||||||
C、λ(
| ||||||||||||
D、若
|
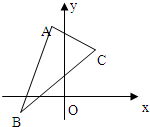 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).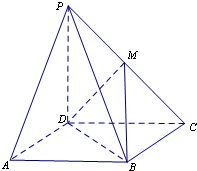 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.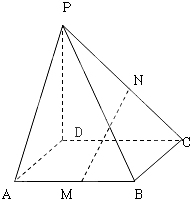 在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;
在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;