题目内容
函数f（x）=x3-ax在（-∞，1]上递增，则a的范围是（ ）
| A、a＞3 | B、a≥3 |
| C、a＜3 | D、a≤3 |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导数，由题意得不等式，解出即可．
解答：
解：∵f′（x）=3x2-a，
∴f′（1）=3-a≥0，
解得：a≤3，
故选：D．
∴f′（1）=3-a≥0，
解得：a≤3，
故选：D．
点评：本题考察了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
函数f（x）=
在点（x0，f（x0））处的切线平行于x轴，则f（x0）等于（ ）
| lnx |
| x |
A、-
| ||
B、
| ||
C、
| ||
| D、e2 |
在独立性检验中，若随机变量k2≥6.635，则（ ）
| A、x与y有关系，犯错的概率不超过1% |
| B、x与y有关系，犯错的概率超过1% |
| C、x与y没有关系，犯错的概率不超过1% |
| D、x与y没有关系，犯错的概率超过1% |
定义两个平面向量的一种新运算
?
=|
|•|
|sin＜
，
＞，（其中＜
，
＞表示
，
的夹角），则对于两个平面向量
，
，下列结论不一定成立的是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||||||||||
B、（
| ||||||||||||
C、λ（
| ||||||||||||
D、若
|
圆M：x2+y2=1与圆N：x2+（y-2）2=1的圆心距|MN|为（ ）
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
已知函数f（x）=x3+ax2-x+c（x∈R），下列结论错误的是（ ）
| A、函数f（x）一定存在极大值和极小值 | ||||
B、若函数f（x）在（-∞，x1），（x2，+∞）上是增函数，则x2-x1≥
| ||||
| C、函数f（x）的图象是中心对称图形 | ||||
| D、函数f（x）一定存在三个零点 |
设P和Q是两个集合，定义集合P-Q={x|x∈P且x∉Q}，如果P={x|x2-2x＜0}，Q={x|1≤x＜3}，那么P-Q=（ ）
| A、{x|0＜x＜1} |
| B、{x|0＜x≤1} |
| C、{x|1≤x＜2} |
| D、{x|2≤x＜3} |
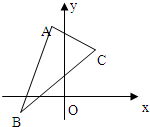已知△ABC三个顶点是A（-1，4），B（-2，-1），C（2，3）．