题目内容
设函数f(x)=
,类比课本推导等差数列前n项和公式的推导方法计算f(-4)+f(-3)+…+f(0)+f(1)+…+f(4)+f(5)的值为( )
| 1 | ||
2x+
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:类比推理
专题:规律型,等差数列与等比数列
分析:根据课本中推导等差数列前n项和的公式的方法--倒序相加法,观察所求式子的特点,应先求f(x)+f(1-x)的值.
解答:
解:∵f(x)=
,
∴f(x)+f(1-x)=
+
=
+
=
+
=
=
,
即 f(-4)+f(5)=
,
f(-3)+f(4)=
,
f(-2)+f(3)=
,
f(-1)+f(2)=
,
f(0)+f(1)=
,
∴f(-4)+f(-3)+…+f(0)+f(1)+…+f(4)+f(5)=
.
故选B.
| 1 | ||
2x+
|
∴f(x)+f(1-x)=
| 1 | ||
2x+
|
| 1 | ||
21-x+
|
| 1 | ||
2x+
|
| 2x | ||
2+
|
| ||
2+
|
| 2x | ||
2+
|
| ||
2+
|
| ||
| 2 |
即 f(-4)+f(5)=
| ||
| 2 |
f(-3)+f(4)=
| ||
| 2 |
f(-2)+f(3)=
| ||
| 2 |
f(-1)+f(2)=
| ||
| 2 |
f(0)+f(1)=
| ||
| 2 |
∴f(-4)+f(-3)+…+f(0)+f(1)+…+f(4)+f(5)=
5
| ||
| 2 |
故选B.
点评:本题为规律性的题目,要善于观察式子的特点,并且此题给出了明确的方法,从而降低了本题难度.

练习册系列答案
相关题目
函数f(x)=
(x∈R)( )
| 4x |
| x2+1 |
| A、既有最大值2,又有最小值-2 |
| B、无最大值,但有最小值-2 |
| C、有最大值2,但无最小值 |
| D、既无最大值,又无最小值 |
如图,A1B1C1-ABC是三棱柱,下列直线中与AA1成异面直线的是( )


| A、BB1 |
| B、CC1 |
| C、B1C1 |
| D、AB |
在独立性检验中,若随机变量k2≥6.635,则( )
| A、x与y有关系,犯错的概率不超过1% |
| B、x与y有关系,犯错的概率超过1% |
| C、x与y没有关系,犯错的概率不超过1% |
| D、x与y没有关系,犯错的概率超过1% |
已知等差数列{an}中,a2=4,a6=12,则公差d等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
定义两个平面向量的一种新运算
?
=|
|•|
|sin<
,
>,(其中<
,
>表示
,
的夹角),则对于两个平面向量
,
,下列结论不一定成立的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||||||||||
B、(
| ||||||||||||
C、λ(
| ||||||||||||
D、若
|
已知函数f(x)=x3+ax2-x+c(x∈R),下列结论错误的是( )
| A、函数f(x)一定存在极大值和极小值 | ||||
B、若函数f(x)在(-∞,x1),(x2,+∞)上是增函数,则x2-x1≥
| ||||
| C、函数f(x)的图象是中心对称图形 | ||||
| D、函数f(x)一定存在三个零点 |
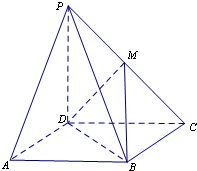 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,点M为PC的中点.