题目内容
在平面直角坐标系xOy中,圆C1:x2+y2-4x-8y+19=0关于直线l:x+2y-5=0对称的圆C2的方程为 .
考点:圆的一般方程
专题:计算题,直线与圆
分析:圆C1化为标准方程,求出圆心坐标与半径,设出圆心C1关于直线l:x+2y-5=0对称的圆C2的圆心C2的坐标,利用对称关系,求出圆心C2的坐标,即可得到圆C2的方程.
解答:
解:圆C1:x2+y2-4x-8y+19=0可化为(x-2)2+(y-4)2=1,则圆心C1(2,4),半径为1,
设圆心C1关于直线l:x+2y-5=0对称的圆C2的圆心C2的坐标为(a,b),则
,解得a=0,b=0,
∴圆C1:x2+y2-4x-8y+19=0关于直线l:x+2y-5=0对称的圆C2的方程为x2+y2=1.
故答案为:x2+y2=1.
设圆心C1关于直线l:x+2y-5=0对称的圆C2的圆心C2的坐标为(a,b),则
|
∴圆C1:x2+y2-4x-8y+19=0关于直线l:x+2y-5=0对称的圆C2的方程为x2+y2=1.
故答案为:x2+y2=1.
点评:本题考查圆的方程,考查点关于直线对称点的求法,考查学生的计算能力,属于中档题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
已知幂函数y=x
(|p|、|q|是互质的整数)的图象如图所示,则p、q的关系为( )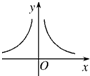
| p |
| q |

| A、pq>0,p、q均为奇数 |
| B、pq<0,p、q均为奇数 |
| C、pq<0,p为奇数,q为偶数 |
| D、pq<0,p为偶数,q为奇数 |
 函数y=Asin(ωx+φ)
函数y=Asin(ωx+φ)