题目内容
过点P(-2,4)作圆O:(x-2)2+(y-1)2=25的切线l,直线m:ax-3y=0与直线l平行,则直线l与m的距离为( )
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
考点:直线与圆相交的性质
专题:直线与圆
分析:判断P在圆O上,求出直线OP的斜率,确定出切线l的斜率,求出l的方程,根据直线m与直线l平行,利用平行线的距离公式求出l与m的距离即可.
解答:
解:将P(-2,4)代入圆方程左边得:42+32=16+9=25,左边=右边,即P在圆O上,
∵直线OP的斜率为
=-
,
∴切线l的斜率为
,即直线l方程为y-4=
(x+2),
整理得:4x-3y+20=0,
∵直线m:ax-3y=0与直线l平行,
∴
=
,即a=4,
∴直线m方程为4x-3y=0,即4x-3y=0,
则直线l与m的距离为
=4.
故选:A.
∵直线OP的斜率为
| 4-1 |
| -2-2 |
| 3 |
| 4 |
∴切线l的斜率为
| 4 |
| 3 |
| 4 |
| 3 |
整理得:4x-3y+20=0,
∵直线m:ax-3y=0与直线l平行,
∴
| a |
| 3 |
| 4 |
| 3 |
∴直线m方程为4x-3y=0,即4x-3y=0,
则直线l与m的距离为
| |-8-12| | ||
|
故选:A.
点评:此题考查了直线与圆相交的性质,圆的切线方程,两直线平行时斜率满足的关系,点到直线的距离公式,弄清题意是解本题的关键.

练习册系列答案
相关题目
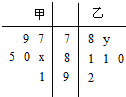 某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )
某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的众数是85,乙班学生成绩的平均分为81,则x+y的值为( )| A、6 | B、7 | C、8 | D、9 |
已知函数f(x)=2x(x∈R)的反函数为f-1(x),则f-1(1)等于( )
| A、0 | B、1 | C、2 | D、4 |
双曲线x2-y2=8的左右焦点分别是F1,F2,点Pn(xn,yn)(n=1,2,3…)在其右支上,且满足|Pn+1F2|=|PnF1|,P1F2⊥F1F2,则x2014的值是( )
A、8056
| ||
B、8048
| ||
| C、8056 | ||
| D、8048 |
已知不等式|x-3|+|x-4|≥m的解集为R,则实数m的取值范围( )
| A、m<1 | ||
| B、m≤1 | ||
C、m≤
| ||
D、m<
|
