Question

设圆x²+y²=a²+b²与双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）在第一象限的交点为P，若双曲线的左、右焦点分别为F₁、F₂，且tan∠PF₂F₁=

3

2

，则双曲线的离心率为

 

．

Answer 1

考点：双曲线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：由已知条件推导出F₁，F₂分别是圆与x轴的交点，PF₁⊥PF₂，|PF₁|=6a，|PF₂|=4a，由此利用勾股定理能求出双曲线的离心率．

解答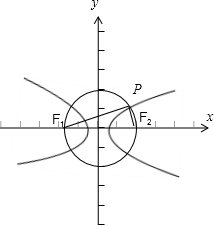： 解：如图，∵圆x²+y²=a²+b²与双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）在第一象限的交点为P，双曲线的左右焦点分别为F₁、F₂，
∴F₁，F₂分别是圆与x轴的交点，
∴PF₁⊥PF₂，
∵tan∠PF₂F₁=

3

2

，
∴

|PF1|

|PF2|

=

3

2

，
由双曲线定义知：
|PF₁|-|PF₂|=

1

2

|PF2|=2a，
∴|PF₁|=6a，|PF₂|=4a，
∵PF₁⊥PF₂，
∴|PF₁|²+|PF₂|²=|F₁F₂|²，
∴（6a）²+（4a）²=（2c）²，
解得c=

13

a，
∴e=

c

a

=

13

．
故答案为：

13

．

点评：本题考查双曲线的离心率的求法，是中档题，解题时要认真审题，注意数形结合思想的合理运用．