题目内容

已知抛物线y2=2px（p＞0）上的一点，M到定点A（
7
2
，4）和焦点F的距离之和的最小值等于5，则抛物线的方程为
 
．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由M到定点A（
7
2
，4）和焦点F的距离之和的最小值等于5，可得M到定点A（
7
2
，4）与它到准线的距离之和的最小值等于5，求出p的值，可得抛物线的方程．
解答： 解：当点A在抛物线内部时，抛物线y2=2px的准线方程为x=-
p
2
．
∵M到定点A（
7
2
，4）和焦点F的距离之和的最小值等于5，
∴M到定点A（
7
2
，4）与它到准线的距离之和的最小值等于5，
∴
7
2
+
p
2
=5，
∴p=3，
∴抛物线的方程为y2=6x．
同理，当点A在抛物线外部或在抛物线上时，抛物线的方程为y2=2x
故答案为：y2=6x或y2=2x．
点评：本题考查抛物线的定义，考查学生分析转化问题的能力，正确运用抛物线的定义是关键．
练习册系列答案
相关题目
已知
a
与
b
的夹角是60°，
a
=（2，0），
b
=（sinθ，cosθ），则|
a
+2
b
|=
 
．
设f-1（x）是函数f（x）=
1
2
（ax-a-x）（a＞1）的反函数，则使f-1（x）＞1成立的x的取值范围是
 
．
在平面直角坐标系xOy中，圆C1：x2+y2-4x-8y+19=0关于直线l：x+2y-5=0对称的圆C2的方程为
 
．
中心在坐标原点，焦点在y轴上的双曲线的渐近线过点P（2，1），其离心率为
 
．
若不等式|x+1|+|x-4|≥a+
4
a
对任意的实数x恒成立，则实数a的取值范围是
 
．
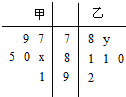某学校从高二甲、乙两个班中各选6名同掌参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生成绩的众数是85，乙班学生成绩的平均分为81，则x+y的值为（　　）
A、6B、7C、8D、9
给出下列命题，其中真命题的个数是（　　）
①存在x0∈R，使得sinx0+cosx0=2sin
7π
24
成立；
②对于任意的三个平面向量
a
、
b
、
c
，总有（
a
•
b
）•
c
=
a
•（
b
•
c
）成立；
③相关系数r（|r|≤1），|r|值越大，变量之间的线性相关程度越高．
A、0B、1C、2D、3
已知n为正偶数，用数学归纳法证明1-
1
2
+
1
3
-
1
4
+…+
1
n-1
-
1
n
=2(
1
n+2
+
1
n+4
+…+
1
2n
)时，第一步应验证（　　）
A、1=2×
1
2
B、1-
1
2
+
1
3
=2(
1
1+2
+
1
2+4
)
C、1-
1
2
+
1
3
-
1
4
=2(
1
4+2
+
1
4+4
)
D、1-
1
2
=2×
1
2+2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网