题目内容
已知幂函数y=x
(|p|、|q|是互质的整数)的图象如图所示,则p、q的关系为( )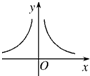
| p |
| q |

| A、pq>0,p、q均为奇数 |
| B、pq<0,p、q均为奇数 |
| C、pq<0,p为奇数,q为偶数 |
| D、pq<0,p为偶数,q为奇数 |
考点:幂函数的概念、解析式、定义域、值域
专题:函数的性质及应用
分析:由已知条件推导出函数为偶函数,p为偶数,q为奇数.再利用导数的性质推导出pq<0.
解答:
解:如图,∵函数的图象关于y轴对称,
∴函数为偶函数,
p为偶数,
∵函数y=x
在(0,+∞)上是减函数,
∴它的导函数y′=
x
<0,
∴
<0.∴pq<0,
∵p、q互质,∴q为奇数.
故选:D.
∴函数为偶函数,
p为偶数,

∵函数y=x
| p |
| q |
∴它的导函数y′=
| p |
| q |
| p-q |
| q |
∴
| p |
| q |
∵p、q互质,∴q为奇数.
故选:D.
点评:本题考查幂函函数的图象及性质的应用,是中档题,解题时要熟练掌握幂函数的概念.

练习册系列答案
相关题目
双曲线x2-y2=8的左右焦点分别是F1,F2,点Pn(xn,yn)(n=1,2,3…)在其右支上,且满足|Pn+1F2|=|PnF1|,P1F2⊥F1F2,则x2014的值是( )
A、8056
| ||
B、8048
| ||
| C、8056 | ||
| D、8048 |
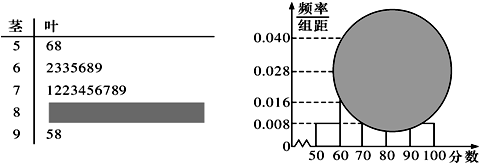
从某校高三数学学业水平测试卷中随机抽取部分试卷,对其成绩进行分析,因某特殊原因,所得的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,则频率分布直方图中,从左往右第四个矩形的面积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线
-
=1(a>0,b>0)与抛物线y2=2px(p>0)的交点为:A、B,A、B连线经过抛物线的焦点F,且线段AB的长等于双曲线的虚轴长,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
| C、3 | ||
D、
|
已知n为正偶数,用数学归纳法证明1-
+
-
+…+
-
=2(
+
+…+
)时,第一步应验证( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n-1 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| n+4 |
| 1 |
| 2n |
A、1=2×
| ||||||||||
B、1-
| ||||||||||
C、1-
| ||||||||||
D、1-
|
已知不等式|x-3|+|x-4|≥m的解集为R,则实数m的取值范围( )
| A、m<1 | ||
| B、m≤1 | ||
C、m≤
| ||
D、m<
|