题目内容
已知四棱锥P-ABCD(图1)的三视图如图2所示,E是侧棱PC上的动点.
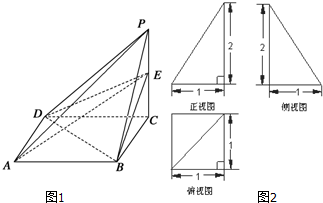
(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(Ⅲ)点E在什么位置时,二面角D-AE-B的大小为120°?

(Ⅰ)求四棱锥P-ABCD的体积;
(Ⅱ)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(Ⅲ)点E在什么位置时,二面角D-AE-B的大小为120°?
考点:用空间向量求平面间的夹角,棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间角
分析:(Ⅰ)求出棱锥的底面积和高,结合棱锥的体积公式,即可求四棱锥P-ABCD的体积;
(Ⅱ)根据线面垂直的性质,只需要证明BD⊥平面PAC即可证明BD⊥AE
(Ⅲ)建立空间直角坐标系,利用向量法,结合二面角D-AE-B的大小为120°,即可确定E的位置.
(Ⅱ)根据线面垂直的性质,只需要证明BD⊥平面PAC即可证明BD⊥AE
(Ⅲ)建立空间直角坐标系,利用向量法,结合二面角D-AE-B的大小为120°,即可确定E的位置.
解答:
解:(Ⅰ)由三视图可知,四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC⊥底面ABCD,且PC=2.
∴VP-ABCD=
SABCD×PC=
×12×2=
.
(Ⅱ)不论点E在何位置,都有ED⊥AE.
证明如下:连接AC.∵PC⊥底面ABCD,且BD⊆底面ABCD,
∴BD⊥PC.又AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,都有AE⊆平面PAC,
∴不论点E在何位置,都有ED⊥AE.
(Ⅲ)解法1:当点E为PC的中点时,二面角D-AE-B的大小为120°.
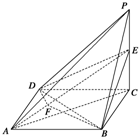
在平面DAE内过点D作DF⊥AE于F,连结EF.
∵AD=AE=1,DE=EF=
,AE=AE=
,
∴Rt△ADE≌Rt△ABE,
从而Rt△ADF≌Rt△AEF,
∴EF⊥AE.
∴∠DFB为二面角D-AE-B的平面角.
在Rt△ADF中,DF=
=
=
,
∴EF=
,又ED=
,
在△DFB中,由余弦定理得cos∠DFB=
=-
,
∴∠DFB=120°,
即二面角D-AE-B的大小为120°.
解法2:如图,以点C为原点,
,
,
所在的直线分别为x,y,z轴建立空间直角坐标系.则D(1,0,0),A(1,1,0),B(0,1,0),E(0,0,1),从而
=(0,1,0),
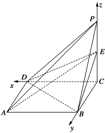
=(-1,0,1),
=(1,0,0),
=(0,-1,1).
设平面ADE和平面ABE的法向量分别为:
=(x1,y1,z1),
=(x2,y2,z2),
由
,即
,取
=(1,0,1),
由
,即
,取
=(0,-1,-1),
设二面角D-AE-F的平面角为θ,则cosθ=
=
=-
,
∴θ=120°,即二面角D-AE-B的大小为120°.
∴VP-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
(Ⅱ)不论点E在何位置,都有ED⊥AE.
证明如下:连接AC.∵PC⊥底面ABCD,且BD⊆底面ABCD,
∴BD⊥PC.又AC∩PC=C,∴BD⊥平面PAC.
∵不论点E在何位置,都有AE⊆平面PAC,
∴不论点E在何位置,都有ED⊥AE.
(Ⅲ)解法1:当点E为PC的中点时,二面角D-AE-B的大小为120°.

在平面DAE内过点D作DF⊥AE于F,连结EF.
∵AD=AE=1,DE=EF=
| 2 |
| 3 |
∴Rt△ADE≌Rt△ABE,
从而Rt△ADF≌Rt△AEF,
∴EF⊥AE.
∴∠DFB为二面角D-AE-B的平面角.
在Rt△ADF中,DF=
| AD•DE |
| AE |
1×
| ||
|
| ||
| 3 |
∴EF=
| ||
| 3 |
| 2 |
在△DFB中,由余弦定理得cos∠DFB=
| DF2+EF2-BD2 |
| 2DF•EF |
| 1 |
| 2 |
∴∠DFB=120°,
即二面角D-AE-B的大小为120°.
解法2:如图,以点C为原点,
| CD |
| CB |
| CP |
| DA |

| DE |
| BA |
| BE |
设平面ADE和平面ABE的法向量分别为:
| n1 |
| n2 |
由
|
|
| n1 |
由
|
|
| n2 |
设二面角D-AE-F的平面角为θ,则cosθ=
| ||||
|
|
| -1 | ||||
|
| 1 |
| 2 |
∴θ=120°,即二面角D-AE-B的大小为120°.
点评:本题主要考查锥体的体积计算,线面垂直的判定,以及二面角的求法,建立坐标系利用向量法是解决本题的关键,运算量较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设某种产品分两道工序生产,第一道工序的次品率为10%,第二道工序的次品率为3%.生产这种产品只要有一道工序出次品就出次品,则该产品的次品率是( )
| A、0.13 | B、0.03 |
| C、0.127 | D、0.873 |
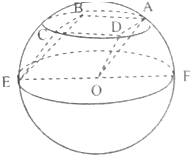 如图,三棱柱OAD-EBC,其中A,B,C,D,E均在以O为球心,半径为2的球面上,EF为直径,侧面ABCD为边长等于2的正方形,则三棱柱OAD-EBC的体积为( )
如图,三棱柱OAD-EBC,其中A,B,C,D,E均在以O为球心,半径为2的球面上,EF为直径,侧面ABCD为边长等于2的正方形,则三棱柱OAD-EBC的体积为( )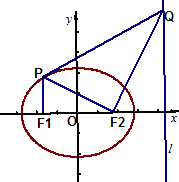 如图,已知椭圆C1:
如图,已知椭圆C1: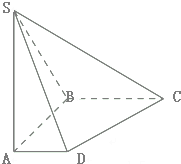 如图,已知在四棱锥S-ABCD中,底面四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=2.
如图,已知在四棱锥S-ABCD中,底面四边形ABCD是直角梯形,∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=2.