题目内容
已知A={x|log2(4x)•log4
≥2},g(x)=
(Ⅰ)求出集合A;
(Ⅱ)判断g(x)的单调性,并用单调性的定义证明;
(Ⅲ)当λ为何值时,方程g(x)=λ在x∈A上有实数解?
| 4 |
| x2 |
| 4x |
| 4x+1 |
(Ⅰ)求出集合A;
(Ⅱ)判断g(x)的单调性,并用单调性的定义证明;
(Ⅲ)当λ为何值时,方程g(x)=λ在x∈A上有实数解?
考点:函数单调性的判断与证明,对数的运算性质,根的存在性及根的个数判断
专题:函数的性质及应用
分析:(Ⅰ)求出集合A中的不等式的解集,即得集合A;
(Ⅱ)用单调性的定义证明g(x)的单调性;
(Ⅲ)由g(x)的单调性,求出g(x)在[
,1]上的最值,即可得出λ的取值范围是什么时,方程g(x)=λ在x∈A上有实数解.
(Ⅱ)用单调性的定义证明g(x)的单调性;
(Ⅲ)由g(x)的单调性,求出g(x)在[
| 1 |
| 2 |
解答:
解:(Ⅰ)集合A中的不等式可化为(2+log2x)(1-log2x)≥2,
整理得,log22x+log2x≤0;
解得,-1≤log2x≤0,
∴
≤x≤1;
∴A=[
,1];
(Ⅱ)g(x)的定义域为R,
设x1>x2,则4x1-4x2>0;
∴g(x1)-g(x2)=
-
=
>0,
∴g(x)在R上是增函数.
(Ⅲ)当x∈[
,1]时,g(x)是增函数,
∴当x=
时,g(x)min=
;当x=1时,g(x)max=
;
∴当
≤λ≤
时,方程g(x)=λ在x∈A上有实数解.
整理得,log22x+log2x≤0;
解得,-1≤log2x≤0,
∴
| 1 |
| 2 |
∴A=[
| 1 |
| 2 |
(Ⅱ)g(x)的定义域为R,
设x1>x2,则4x1-4x2>0;
∴g(x1)-g(x2)=
| 4x1 |
| 4x1+1 |
| 4x2 |
| 4x2+1 |
| 4x1-4x2 |
| (4x1+1)(4x2+1) |
∴g(x)在R上是增函数.
(Ⅲ)当x∈[
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 2 |
| 3 |
| 4 |
| 5 |
∴当
| 2 |
| 3 |
| 4 |
| 5 |
点评:本题考查了函数与不等式和方程的解法与应用问题,解题时应根据函数的单调性求不等式的解集,求函数的最值,从而判定方程的解是否存在,是综合性题目.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
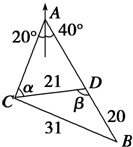 C位于A城的南偏西20°的位置,B位于A城的南偏东40°的位置,有一人距C为31千米的B处正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?
C位于A城的南偏西20°的位置,B位于A城的南偏东40°的位置,有一人距C为31千米的B处正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?