题目内容
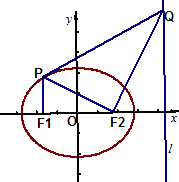 如图,已知椭圆C1:
如图,已知椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(Ⅰ)求椭圆C1的方程;
(Ⅱ)证明:直线PQ与椭圆C1只有一个交点;
(Ⅲ)若过直线l:x=4
| 2 |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:压轴题,存在型
分析:对第(1)问,由已知条件寻找PF1或PF2与圆的直径的关系,再利用椭圆的定义,可得a2,b2;
对第(2)问,设出Q点的坐标,由PF2⊥QF2得Q的坐标,从而得直线PQ的方程,联立直线与椭圆的方程,只需证判别式△=0即可;
对第(3)问,先设出A点的坐标,再设法用此坐标建立直线MN的方程,根据直线方程的形式特点可获取定点.
对第(2)问,设出Q点的坐标,由PF2⊥QF2得Q的坐标,从而得直线PQ的方程,联立直线与椭圆的方程,只需证判别式△=0即可;
对第(3)问,先设出A点的坐标,再设法用此坐标建立直线MN的方程,根据直线方程的形式特点可获取定点.
解答:
解:(Ⅰ)∵△PF1F2为直角三角形,∴斜边PF2为圆C2的直径.
设圆C2与y轴交于点B,D,圆心为点C,
∵PF1∥y轴,坐标原点O为线段F1F2的中点,
∴圆心C2即为PF2与y轴的交点,从而BD也是圆C2的直径.
由题意知|BD|=|PF2|=6=3|PF1|,得|PF1|=2,
根据椭圆的定义,有|PF1|+|PF2|=2a,则2a=2+6,得a2=16,
在直角△PF1F2中,由勾股定理有|F1F2|2=|PF2|2-|PF1|2,
即(2c)2=32,∴c2=8,从而b2=a2-c2=8,
故椭圆C1的方程为
+
=1.
(Ⅱ)设Q(4
,y0),易知P(-2
,2),F2(2
,0),
由F2P⊥F2Q,得
•
=0,
即(-4
,2)•(2
,y0)=0,得y0=8.
则PQ的斜率kPQ=
=
,从而直线PQ的方程为y-2=
(x+2
),
即y=
x+4,联立
+
=1,消去y并整理得x2+4
x+8=0,
∵△=(4
)2-32=0,∴直线PQ与椭圆C1相切,即直线PQ与椭圆C1只有一个交点.
(Ⅲ)设切点M(x1,y1),N(x2,y2),A(4
,t),
由(Ⅱ)知圆C2的方程为x2+(y-1)2=9,即x2+y2-2y-8=0,
则切线AM的方程为x1x+y1y-2•
-8=0,即x1x+(y1-1)y-y1-8=0,
同理,切线AN的方程为x2x+(y2-1)y-y2-8=0,
将A点坐标分别代入AM,AN的方程中,得
,
于是M,N的坐标都满足方程4
x+(y-1)t-y-8=0,即4
x-y-8+(y-1)t=0,
根据两点确定一条直线,MN的方程就是4
x-y-8+(y-1)t=0,
当
即
时,MN的方程对t∈R恒成立,
故直线恒过定点(
,1).
设圆C2与y轴交于点B,D,圆心为点C,
∵PF1∥y轴,坐标原点O为线段F1F2的中点,
∴圆心C2即为PF2与y轴的交点,从而BD也是圆C2的直径.
由题意知|BD|=|PF2|=6=3|PF1|,得|PF1|=2,
根据椭圆的定义,有|PF1|+|PF2|=2a,则2a=2+6,得a2=16,
在直角△PF1F2中,由勾股定理有|F1F2|2=|PF2|2-|PF1|2,
即(2c)2=32,∴c2=8,从而b2=a2-c2=8,
故椭圆C1的方程为
| x2 |
| 16 |
| y2 |
| 8 |
(Ⅱ)设Q(4
| 2 |
| 2 |
| 2 |
由F2P⊥F2Q,得
| F2P |
| F2Q |
即(-4
| 2 |
| 2 |
则PQ的斜率kPQ=
| 8-2 | ||||
4
|
| ||
| 2 |
| ||
| 2 |
| 2 |
即y=
| ||
| 2 |
| x2 |
| 16 |
| y2 |
| 8 |
| 2 |
∵△=(4
| 2 |
(Ⅲ)设切点M(x1,y1),N(x2,y2),A(4
| 2 |
由(Ⅱ)知圆C2的方程为x2+(y-1)2=9,即x2+y2-2y-8=0,
则切线AM的方程为x1x+y1y-2•
| y1+y |
| 2 |
同理,切线AN的方程为x2x+(y2-1)y-y2-8=0,
将A点坐标分别代入AM,AN的方程中,得
|
于是M,N的坐标都满足方程4
| 2 |
| 2 |
根据两点确定一条直线,MN的方程就是4
| 2 |
当
|
|
故直线恒过定点(
9
| ||
| 8 |
点评:1.本题已知条件众多,应充分利用题中给出的信息,并注意信息与信息之间的联系,另外,确定椭圆方程时,
不可忽略条件a2=b2+c2.
2.判断直线与椭圆的位置关系时,常联立直线与椭圆的方程,消去x或y,得到一个关于y或x的一元二次方程,根据判别式△的符号下结论.
3.直线与圆相切是直线与圆的一种很重要的位置关系,熟记一些常用的规律,可减少许多繁琐的计算量,如过圆x2+y2+Dx+Ey+F=0上一点(x0,y0)的圆的切线方程为x0x+y0y+D•
+E•
+F=0,即x2用x0x代,y2用y0y代,x用
代,y用
代,此规律不仅适合于圆,也适合于椭圆,抛物线等.
4.判断直线是否过定点,常从直线方程的形式入手,采用分离参数法处理.
不可忽略条件a2=b2+c2.
2.判断直线与椭圆的位置关系时,常联立直线与椭圆的方程,消去x或y,得到一个关于y或x的一元二次方程,根据判别式△的符号下结论.
3.直线与圆相切是直线与圆的一种很重要的位置关系,熟记一些常用的规律,可减少许多繁琐的计算量,如过圆x2+y2+Dx+Ey+F=0上一点(x0,y0)的圆的切线方程为x0x+y0y+D•
| x0+x |
| 2 |
| y0+y |
| 2 |
| x0+x |
| 2 |
| y0+y |
| 2 |
4.判断直线是否过定点,常从直线方程的形式入手,采用分离参数法处理.

练习册系列答案
相关题目
已知
=(1,1,0),
=(-1,0,2),且k
+
与2
-
垂直,则k的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
| B、1 | ||
C、
| ||
D、
|
已知向量
,
是夹角为60°的两个单位向量,向量
+λ
(λ∈R)与向量
-2
垂直,则实数λ的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、2 | D、0 |
已知向量
、
的夹角为45°,且|
|=1,|2
-
|=
,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| 10 |
| b |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
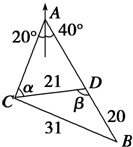 C位于A城的南偏西20°的位置,B位于A城的南偏东40°的位置,有一人距C为31千米的B处正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?
C位于A城的南偏西20°的位置,B位于A城的南偏东40°的位置,有一人距C为31千米的B处正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?