题目内容
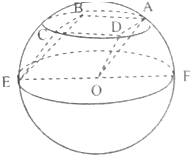如图，三棱柱OAD-EBC，其中A，B，C，D，E均在以O为球心，半径为2的球面上，EF为直径，侧面ABCD为边长等于2的正方形，则三棱柱OAD-EBC的体积为（ ）A、4
| ||
B、4
| ||
C、2
| ||
D、2
|
考点：球的体积和表面积
专题：空间位置关系与距离
分析：连结OB，OC，判断O-ABCD的形状，求出体积，利用三棱锥的体积与三棱柱体积的关系，求出结果．
解答：
解：连结OB，OC，由题意可知O-ABCD是棱长为2的四棱锥，O到底面ABCD的距离为h=
=
．
VO-ABCD=
SABCD•h=
×2×2×
=
．
三棱柱OAD-EBC的体积为：
×
=2
．
故选：D．
解：连结OB，OC，由题意可知O-ABCD是棱长为2的四棱锥，O到底面ABCD的距离为h=A02-(
|
22-(
|
VO-ABCD=
| 1 |
| 3 |
| 1 |
| 3 |
22-(
|
4
| ||
| 3 |
三棱柱OAD-EBC的体积为：
| 3 |
| 2 |
4
| ||
| 3 |
| 2 |
故选：D．
点评：本题考查球与内接几何体的关系，三棱柱与三棱锥的体积的求法以及关系的应用，考查转化思想．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
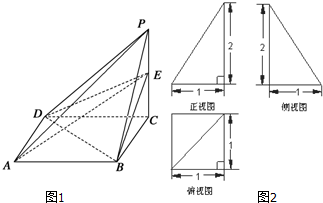
三棱椎的三视图为如图所示的三个直角三角形，则三棱锥的表面积为（ ）
A、4+4
| ||||
B、2+2
| ||||
C、
| ||||
D、2+2
|
已知向量
=（cos75°，sin75°），
=（cos15°，sin15°），那么|
+2
|的值为（ ）
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
已知向量
，
是夹角为60°的两个单位向量，向量
+λ
（λ∈R）与向量
-2
垂直，则实数λ的值为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | B、-1 | C、2 | D、0 |
在钝角三角形ABC中，若B=45°，a=
，则边长c的取值范围是（ ）
| 2 |
A、（1，
| ||
B、（0，1）∪（
| ||
| C、（1，2） | ||
| D、（0，1）∪（2，+∞） |
已知向量
、
的夹角为45°，且|
|=1，|2
-
|=
，则|
|=（ ）
| a |
| b |
| a |
| a |
| b |
| 10 |
| b |
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
