题目内容
 函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤
函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤| π |
| 2 |
A、
| ||
| B、5 | ||
C、
| ||
| D、1 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:利用y=Asin(ωx+φ)的图象特征,求出函数y=Asin(ωx+φ)的解析式,再根据y=Asin(ωx+φ)的图象变换规律,求得m的最小值.
解答:
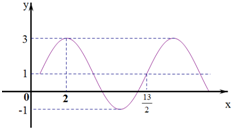
解:由图可知A=2,h=1,
T=
•
=
-2,∴?=
.
再根据五点法作图可得
×2+φ=
,∴φ=-
,∴f(x)=2sin(
x-
)+1.
将f(x)向右平移m个单位后为g(x)=2sin[
(x-m)-
]+1=2sin(
x-
m-
)+1.
若g(x)为偶函数,则-
m-
=kπ+
,(k∈Z),
得m=-(3k+2),(k∈Z,m>0),∴m的最小值为1,
故选:D.
| 3 |
| 4 |
| 3 |
| 4 |
| 2π |
| ? |
| 13 |
| 2 |
| π |
| 3 |
再根据五点法作图可得
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
将f(x)向右平移m个单位后为g(x)=2sin[
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
若g(x)为偶函数,则-
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
得m=-(3k+2),(k∈Z,m>0),∴m的最小值为1,
故选:D.
点评:本题主要考查y=Asin(ωx+φ)的图象变换规律,由函数y=Asin(ωx+φ)的部分图象求解析式,属于中档题.

练习册系列答案
相关题目
在五个数字1,2,3,4,5中,若随机取出三个数字,则剩下两个数字的和是奇数的概率是( )
| A、0.3 | B、0.4 |
| C、0.5 | D、0.6 |
下列函数中周期为π且图象关于直线x=
对称的函数是( )
| π |
| 3 |
A、y=2sin(
| ||||
B、y=2sin(2x-
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(
|
下列说法正确的是( )
| A、若已知两个变量具有线性相关关系,且它们正相关,则其线性回归直线的斜率为正 |
| B、直线l垂直于平面α的充要条件为l垂直于平面α内的无数条直线 |
| C、若随机变量ξ~N(10,0.12),且P(9.9<ξ<10.1)=0.6826,则P(ξ>10.1)=0.3174 |
| D、已知命题P:?x∈R,x2-2x+2>0,则¬p:?x∈R,x2-2x+2<0 |
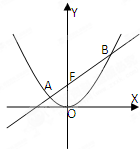 抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点
抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点