题目内容
已知球O夹在一个锐二面角α-l-β之间，与两个半平面分别相切于点A、B，若AB=
，球心O到该二面角的棱l的距离为
，则球O的体积为 ．
4
| ||
| 5 |
| 5 |
考点：球的体积和表面积
专题：球
分析：设球的半径为r．过球心O作直线l的垂线，设垂足为C，则三角形OAC是以角A为直角的直角三角形，求出点A到OC的距离，设AC的长为x，通过三角形面积求出r=1，然后求出球的体积．
解答：
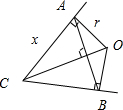解：设球的半径为r．过球心O作直线l的垂线，
设垂足为C，则三角形OAC是以角A为直角的直角三角形，且OA=r，OC=
，
点A到OC的距离为
，
设AC的长为x，则xr=
×
=2，x2+r2=5，
两式联立解得r=1（x=2，）或r=2（x=1，）（∵二面角为锐二面角，故舍去），
∴r=1，
∴球的体积为：
π．
解：设球的半径为r．过球心O作直线l的垂线，设垂足为C，则三角形OAC是以角A为直角的直角三角形，且OA=r，OC=
| 5 |
点A到OC的距离为
2
| ||
| 5 |
设AC的长为x，则xr=
2
| ||
| 5 |
| 5 |
两式联立解得r=1（x=2，）或r=2（x=1，）（∵二面角为锐二面角，故舍去），
∴r=1，
∴球的体积为：
| 4 |
| 3 |
点评：本题考查球的体积的求法，二面角的应用，考查计算能力．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知平面α内有一个以AB为直径的圆，PA⊥α，点C在圆周上（不同于A、B两点），点D、E分别是点A在PC、PB上的射影，则（ ）
| A、PC⊥面ADE |
| B、∠ACB是二面角A-PC-B的平面角 |
| C、BC∥面ADE |
| D、PB⊥面ADE |
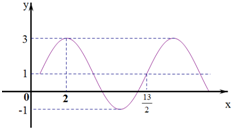函数f（x）=Asin（?x+φ）+h（A＞0，?＞0，|φ|≤