题目内容
已知二次函数f(x)=mx2+(m-3)x+1,对于任意实数x,恒有f(x)≤f(m)(m为常数),求m的值.
考点:二次函数的性质
专题:函数的性质及应用
分析:由已知二次函数f(x)=mx2+(m-3)x+1,对于任意实数x,恒有f(x)≤f(m),可得f(m)为函数的最大值,故m<0且-
=m,解方程可得答案.
| m-3 |
| 2m |
解答:
解:依题意知,m≠0,
∵对于任意实数x,恒有f(x)≤f(m),
∴函数f(x)存在最大值,且最大值为f(m),
∴m<0,
又当x=-
时,函数f(x)=mx2+(m-3)x+1取最大值,
∴-
=m,
解得:m=-
,或m=1(舍去),
故m的值为-
.
∵对于任意实数x,恒有f(x)≤f(m),
∴函数f(x)存在最大值,且最大值为f(m),
∴m<0,
又当x=-
| m-3 |
| 2m |
∴-
| m-3 |
| 2m |
解得:m=-
| 3 |
| 2 |
故m的值为-
| 3 |
| 2 |
点评:本题考查的知识点是二次函数的图象和性质,其中根据已知分析出f(m)为函数的最大值,进而根据二次函数的图象和性质构造方程组,是解答的关键.

练习册系列答案
相关题目

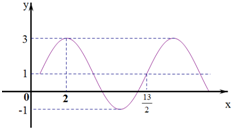 函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤
函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤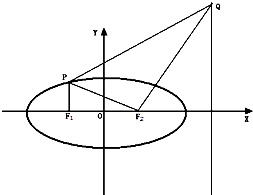 如图,点F1(-c,0)、F2(c,0)分别是椭圆
如图,点F1(-c,0)、F2(c,0)分别是椭圆