题目内容
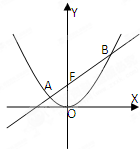 抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点
抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点(1)求抛物线C的方程;
(2)若△AOB的面积为4,求直线l的方程.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由抛物线的定义及点N的纵坐标为1,得|NF|=
+yN=
+1,结合|NF|=2,求出p的值,即可求抛物线C的方程;
(2)设直线l的方程为:y=kx+1,代入抛物线方程,利用弦长公式求出|AB|,再求出O到AB的距离,利用△AOB的面积为4,求出k的值,即可求直线l的方程.
| p |
| 2 |
| p |
| 2 |
(2)设直线l的方程为:y=kx+1,代入抛物线方程,利用弦长公式求出|AB|,再求出O到AB的距离,利用△AOB的面积为4,求出k的值,即可求直线l的方程.
解答:
解:(1)由已知得焦点F(0,
),准线方程为y=-
,
由抛物线的定义及点N的纵坐标为1,得|NF|=
+yN=
+1
又|NF|=2,
∴
+1=2∴p=2,
∴抛物线的方程为x2=4y(4分)
(2)依题意设直线l的方程为:y=kx+1(k必存在)
⇒x2-4kx-4=0,…(6分)
则△=16k2+16>0,
设直线l与抛物线的交点坐标为A(x1,y1),B(x2,y2),
则有x1+x2=4k,x1x2=-4,…(8分)
∴|AB|=
|x1-x2|=
•
=4(1+k2)…(10分)
∵O到AB的距离d=
,
∴S△AOB=
|AB|d=2
=4,
∴k=±
,
∴直线方程为y=±
x+1…..(12分)
| p |
| 2 |
| p |
| 2 |
由抛物线的定义及点N的纵坐标为1,得|NF|=
| p |
| 2 |
| p |
| 2 |
又|NF|=2,
∴
| p |
| 2 |
∴抛物线的方程为x2=4y(4分)
(2)依题意设直线l的方程为:y=kx+1(k必存在)
|
则△=16k2+16>0,
设直线l与抛物线的交点坐标为A(x1,y1),B(x2,y2),
则有x1+x2=4k,x1x2=-4,…(8分)
∴|AB|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
∵O到AB的距离d=
| 1 | ||
|
∴S△AOB=
| 1 |
| 2 |
| k2+1 |
∴k=±
| 3 |
∴直线方程为y=±
| 3 |
点评:本题考查抛物线的定义与方程,考查直线与抛物线的位置关系,考查弦长的计算,考查三角形面积的计算,正确运用韦达定理是关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
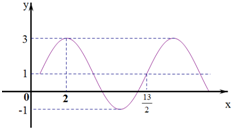 函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤
函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤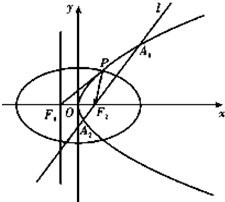 如图,设抛物线
如图,设抛物线