题目内容
下列说法正确的是( )
| A、若已知两个变量具有线性相关关系,且它们正相关,则其线性回归直线的斜率为正 |
| B、直线l垂直于平面α的充要条件为l垂直于平面α内的无数条直线 |
| C、若随机变量ξ~N(10,0.12),且P(9.9<ξ<10.1)=0.6826,则P(ξ>10.1)=0.3174 |
| D、已知命题P:?x∈R,x2-2x+2>0,则¬p:?x∈R,x2-2x+2<0 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:直接由线性正相关的特点得到A正确;
由线面垂直的判定定理得到选项B错误;
由正态分布的概率计算公式求得P(ξ>10.1),从而判断选项C错误;
直接写出全程命题的否定判断选项D错误.
由线面垂直的判定定理得到选项B错误;
由正态分布的概率计算公式求得P(ξ>10.1),从而判断选项C错误;
直接写出全程命题的否定判断选项D错误.
解答:
解:对于选项A,两个变量具有线性相关关系,且它们正相关,则随着x的增大y增大,其线性回归直线的斜率为正,选项A正确;
对于选项B,直线l垂直于平面α内的无数条直线,直线l不一定垂直于平面α,反之,直线l垂直于平面α,则l垂直于平面a内的无数条直线.
∴直线l垂直于平面α是l垂直于平面α内的无数条直线的充分不必要条件.选项B错误;
对于C,若随机变量ξ~N(10,0.12),且P(9.9<ξ<10.1)=0.6826,
则P(ξ>10.1)=
(1-0.6826)=0.1587.选项C错误;
对于选项D,命题P:?x∈R,x2-2x+2>0,则¬p:?x∈R,x2-2x+2≤0.选项D错误.
∴说法正确的是A.
故选A.
对于选项B,直线l垂直于平面α内的无数条直线,直线l不一定垂直于平面α,反之,直线l垂直于平面α,则l垂直于平面a内的无数条直线.
∴直线l垂直于平面α是l垂直于平面α内的无数条直线的充分不必要条件.选项B错误;
对于C,若随机变量ξ~N(10,0.12),且P(9.9<ξ<10.1)=0.6826,
则P(ξ>10.1)=
| 1 |
| 2 |
对于选项D,命题P:?x∈R,x2-2x+2>0,则¬p:?x∈R,x2-2x+2≤0.选项D错误.
∴说法正确的是A.
故选A.
点评:本题考查了命题的真假判断与应用,解答的关键是掌握正态分布的概率计算公式,是中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
已知复数方程
=i(i为虚数单位),则复数z的虚部为( )
| 1+i |
| 3i+z |
| A、2 | B、4i | C、-2 | D、-4 |
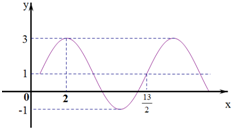 函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤
函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤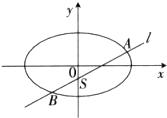 已知F1,F2是椭圆E:
已知F1,F2是椭圆E: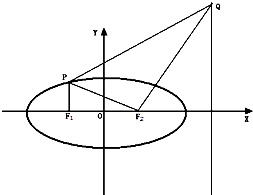 如图,点F1(-c,0)、F2(c,0)分别是椭圆
如图,点F1(-c,0)、F2(c,0)分别是椭圆