题目内容
己知函数f(x)=lnx-ax+1(a>0).
(1)试探究函数f(x)的零点个数;
(2)若f(x)的图象与x轴交于A(x1,0)B(x2,0)(x1<x2)两点,AB中点为C(x0,0),设函数f(x)的导函数为f′(x),求证:f′(x0)<0.
(1)试探究函数f(x)的零点个数;
(2)若f(x)的图象与x轴交于A(x1,0)B(x2,0)(x1<x2)两点,AB中点为C(x0,0),设函数f(x)的导函数为f′(x),求证:f′(x0)<0.
考点:导数在最大值、最小值问题中的应用,函数零点的判定定理
专题:导数的综合应用
分析:(1)中,通过对f(x)求导,研究f(x)的单调性及最值,从而利用数形结合的方法判断零点的个数;
(2)将A、B两点代入到f(x)中,即
,解出a=
,然后写出f'(x0)的表达式,即用x1,x2 表示f'(x0),f'(x0)=
[
-ln
],再令
=t∈(0,1),研究h(t)=
-lnt的性质,从而证明f'(x0)的正负.
(2)将A、B两点代入到f(x)中,即
|
| lnx1-lnx2 |
| x1-x2 |
| 1 |
| x1-x2 |
2(
| ||
|
| x1 |
| x2 |
| x1 |
| x2 |
| 2(t-1) |
| t+1 |
解答:
解:(1)f′(x)=
-a=
,
令f'(x)>0,则0<x<
;令f'(x)<0,则x>
.
∴f(x)在x=a时取得最大值,即f(x)max=f(
)=ln
①当ln
>0,即0<a<1时,考虑到当x无限趋近于0(从0的右边)时,f(x)→-∞;当x→+∞时,f(x)→-∞
∴f(x)的图象与x轴有2个交点,分别位于(0,
)及(
,+∞)
即f(x)有2个零点;
②当ln
=0,即a=1时,f(x)有1个零点;
③当ln
<0,即a>1时f(x)没有零点;
(2)由
得a=
(0<x1<x2),f′(x0)=
-a=
-a=
-
=
[
-ln
],令
=t∈(0,1),设h(t)=
-lnt,t∈(0,1)且h(1)=0
则h′(t)=
-
=
,又t∈(0,1),∴h′(t)<0,∴h(t)>h(1)=0
即
-ln
>0,又
<0,
∴f'(x0)=
[
-ln
]<0.
| 1 |
| x |
| 1-ax |
| x |
令f'(x)>0,则0<x<
| 1 |
| a |
| 1 |
| a |
∴f(x)在x=a时取得最大值,即f(x)max=f(
| 1 |
| a |
| 1 |
| a |
①当ln
| 1 |
| a |
∴f(x)的图象与x轴有2个交点,分别位于(0,
| 1 |
| a |
| 1 |
| a |
即f(x)有2个零点;
②当ln
| 1 |
| a |
③当ln
| 1 |
| a |
(2)由
|
| lnx1-lnx2 |
| x1-x2 |
| 1 |
| x0 |
| 2 |
| x1+x2 |
| 2 |
| x1+x2 |
| lnx1-lnx2 |
| x1-x2 |
| 1 |
| x1-x2 |
2(
| ||
|
| x1 |
| x2 |
| x1 |
| x2 |
| 2(t-1) |
| t+1 |
则h′(t)=
| 4 |
| (t+1)2 |
| 1 |
| t |
| -(t-1)2 |
| (t+1)2t |
即
2(
| ||
|
| x1 |
| x2 |
| 1 |
| x1-x2 |
∴f'(x0)=
| 1 |
| x1-x2 |
2(
| ||
|
| x1 |
| x2 |
点评:本题在导数的综合应用中属于难题,题目中的两个小问都有需要注意之处,如(1)中,在对0<a<1进行研究时,一定要注意到f(x)的取值范围,才能确定零点的个数,否则不能确定.(2)中,代数运算比较复杂,特别是计算过程中,令
=t的化简和换元,使得原本比较复杂的式子变得简单化而可解,这对学生的综合能力有比较高的要求.
| x1 |
| x2 |

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
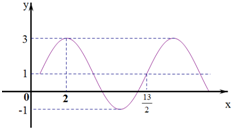 函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤
函数f(x)=Asin(?x+φ)+h(A>0,?>0,|φ|≤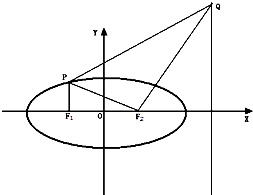 如图,点F1(-c,0)、F2(c,0)分别是椭圆
如图,点F1(-c,0)、F2(c,0)分别是椭圆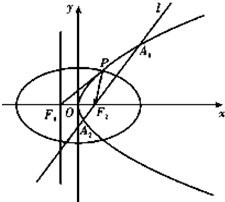 如图,设抛物线
如图,设抛物线