题目内容
一个棱锥的三视图如图所示,则它的体积为


考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据已知三视图,我们结合棱锥的结构特征易判断出几何体为四锥锥,结合三视图中标识的数据,我们易求出棱锥的底面面积及棱锥的高,代入棱锥体积公式即可得到答案.
解答:
解:由已知三视图我们可得:
棱锥以俯视图为底面,
以主视图高为高,故h=1,
S底面=
×(1+2)×1=
,
故V=
S底面h=
,
故答案为:
棱锥以俯视图为底面,
以主视图高为高,故h=1,
S底面=
| 1 |
| 2 |
| 3 |
| 2 |
故V=
| 1 |
| 3 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查的知识点是根据三视图求几何体的体积,其中根据已知三视图,结合简单几何体的结构特征易判断出几何体的形状,和相关的几何量(底面边长,高)是解答本题的关键.

练习册系列答案
相关题目
设曲线y=ax2+2014在点(1,a+2014)处的切线与直线2x-y-2015=0平行,则a=( )
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
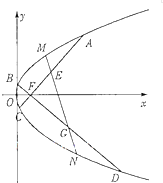 如图,已知点F为抛物线C1:y2=4x的焦点,过点F任作两条互相垂直的直线l1,l2,分别交抛物线C1于A,C,B,D四点,E,G分别为AC,BD的中点.
如图,已知点F为抛物线C1:y2=4x的焦点,过点F任作两条互相垂直的直线l1,l2,分别交抛物线C1于A,C,B,D四点,E,G分别为AC,BD的中点. 如图,设α∈(0,π),且α≠
如图,设α∈(0,π),且α≠