题目内容
二维空间中圆的二维度(面积)S=πr2,一维测度(周长)l=2πr; 三维空间中球的三维测度(体积)V=
πr3,二维测度(表面积)S=4πr2.若四维空间中“超球”的四维测度W=2πr4,根据上述规律,猜想其三维测度(体积)V= .
| 4 |
| 3 |
考点:类比推理
专题:推理和证明
分析:根据二维度数值是2倍关系,三维度数值是3倍关系,得出四维度数值应是4倍关系.
解答:
解:∵圆的二维度(面积)S=πr2,一维测度(周长)l=2πr;
三维空间中球的三维测度(体积)V=
πr3,二维测度(表面积)S=4πr2;
∴四维空间中“超球”的四维测度W=2πr4,三维测度(体积)V=8πr3;
故答案为:8πr3.
三维空间中球的三维测度(体积)V=
| 4 |
| 3 |
∴四维空间中“超球”的四维测度W=2πr4,三维测度(体积)V=8πr3;
故答案为:8πr3.
点评:本题考查了类比推理的应用问题,类比推理是根据两个或两类对象有部分属性相同,从而推出它们的其他属性也相同的推理,是基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.
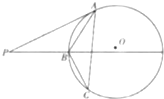 如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=
如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=