题目内容
如图，设α∈（0，π），且α≠| π |
| 2 |
| e1 |
| e2 |
| OP |
| e1 |
| e2 |
| OP |
①
| a |
| a |
| m2+n2 |
②
| a |
| b |
| a |
| b |
③
| a |
| b |
| a |
| b |
| π |
| 3 |
| 2π |
| 3 |
④
| a |
| b |
| a |
| b |
考点：命题的真假判断与应用,平面向量的坐标运算
专题：平面向量及应用,简易逻辑
分析：把新定义回归到向量的数量积的运算对每个结论进行验证，即可得出结论．
解答：
解：对于①，
=（m，n），则|
|=|m
+n
|=
，∵α≠
，∴①错误；
对于②，由
∥
得
=λ
，∴s=λm，t=λn，∴mt-ns=0，故②正确；
对于③，
=（1，2），
（2，1），
与
的夹角为
，根据夹角公式得4+5
•
=（5+4
•
）cos
，故
•
=-
，即cosα=-
，则α=
，③正确
对于④，∵
•
=（m
+n
）•（s
+t
）=ms+nt+（mt+ns）cosα≠ms+nt，∴④错误；
所以正确的是②、③．
故答案为：②③
| a |
| a |
| e1 |
| e2 |
| m2+n2+2mncosα |
| π |
| 2 |
对于②，由
| a |
| b |
| b |
| a |
对于③，
| a |
| b |
| a |
| b |
| π |
| 3 |
| e1 |
| e2 |
| e1 |
| e2 |
| π |
| 3 |
| e1 |
| e2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| 3 |
对于④，∵
| a |
| b |
| e1 |
| e2 |
| e1 |
| e2 |
所以正确的是②、③．
故答案为：②③
点评：本题为新定义，正确理解题中给出的斜坐标并与已知的向量知识相联系是解决问题的关键，属基础题．
练习册系列答案
相关题目
如图，AB是圆O的直径，点C是圆O上异于A、B的点，直线PC⊥平面ABC，E，F分别为PA，PC的中点．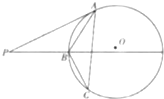
如图，过圆O外一点P分别作圆的切线和割线交圆于A，B，且PB=9，C是圆上一点使得BC=4，∠BAC=∠APB，则AB=
已知在△ABC中，D是BC边上的中点，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F，S△FCD=5，BC=10，则DE=（ ）