题目内容
设曲线y=ax2+2014在点（1，a+2014）处的切线与直线2x-y-2015=0平行，则a=（ ）
| A、1 | ||
B、
| ||
C、-
| ||
| D、-1 |
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：利用曲线在切点处的导数为斜率求曲线的切线斜率，利用直线平行它们的斜率相等列方程，即可求出a的值．
解答：
解：求导函数y′=2ax，
∴x=1时，y′=2a，
∵曲线y=ax2+2014在点（1，a+2014）处的切线与直线2x-y-2015=0平行，
∴有2a=2
∴a=1
故选：A．
∴x=1时，y′=2a，
∵曲线y=ax2+2014在点（1，a+2014）处的切线与直线2x-y-2015=0平行，
∴有2a=2
∴a=1
故选：A．
点评：本题考查两条直线平行，考查导数的几何意义：曲线在切点处的导数值是切线的斜率．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
若平面α∥平面β，直线a∥平面α，点B∈β，则在平面β内且过B点的所有直线中（ ）
| A、不一定存在与a平行的直线 |
| B、只有两条与a平行的直线 |
| C、存在无数条与a平行的直线 |
| D、存在唯一与a平行的直线 |
已知在△ABC中，D是BC边上的中点，且AD=AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F，S△FCD=5，BC=10，则DE=（ ）x=2是x2-4x+4=0的（ ）
| A、充分条件 |
| B、必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
“a=1”是“函数f（x）=（x-1）2在区间[a，+∞）上为增函数”的（ ）
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
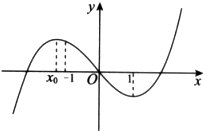函数f（x）=ax3-bx2+cx的图象如图所示，且f（x）在x=x0与x=1处取得极值，给出下列判断：①c＞0；
②f（1）+f（-1）＞0；
③函数y=f′（x）在区间（0，+∞）上是增函数．
其中正确的判断是（ ）
| A、①③ | B、② | C、②③ | D、①② |
如图为正方体表面的一种展开图，则图中的四条线段AB，CD，EF，GH在原正方体中互为异面的对数为（ ）| A、1 | B、2 | C、3 | D、4 |