题目内容
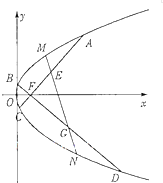 如图,已知点F为抛物线C1:y2=4x的焦点,过点F任作两条互相垂直的直线l1,l2,分别交抛物线C1于A,C,B,D四点,E,G分别为AC,BD的中点.
如图,已知点F为抛物线C1:y2=4x的焦点,过点F任作两条互相垂直的直线l1,l2,分别交抛物线C1于A,C,B,D四点,E,G分别为AC,BD的中点.(Ⅰ)当直线AC的斜率为2时,求直线EG的方程;
(Ⅱ)直线EG是否过定点?若过,求出该定点;若不过,说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)F(1,0),设A(x1,y1),C(x2,y2),当直线AC的斜率为2时,直线AC的方程为x=
y+1,代入抛物线C1的方程,得y2-2y-4=0,求出AC的中点坐标E(
,1),同理得BD的中点坐标为G(9,-4),由此能求出直线EG的方程.
(Ⅱ)直线EG过定点(3,0),设A(x3,y3),C(x4,y4),直线AC的方程为x=my+1,代入抛物线C1的方程,得y2-4my-4=0,由此能求出直线过定点H(3,0).
| 1 |
| 2 |
| 3 |
| 2 |
(Ⅱ)直线EG过定点(3,0),设A(x3,y3),C(x4,y4),直线AC的方程为x=my+1,代入抛物线C1的方程,得y2-4my-4=0,由此能求出直线过定点H(3,0).
解答:
解:(Ⅰ)∵F为抛物线C1:y2=4x的焦点,∴F(1,0),
设A(x1,y1),C(x2,y2),当直线AC的斜率为2时,
直线AC的方程为x=
y+1,
代入抛物线C1的方程,得y2-2y-4=0,
设A(x1,y1),C(x2,y2),
则y1+y2=2,∴x1+x2=(
y1+1)+(
y2+1)=3,
∴AC的中点坐标E(
,1),
由AC⊥BD,得直线BD的方程为x=-2y+1,
同理,得BD的中点坐标为G(9,-4),
由E(
,1),G(9,-4)得直线EG的方程为2x+3y-6=0.
(Ⅱ)直线EG过定点(3,0),设A(x3,y3),C(x4,y4),
直线AC的方程为x=my+1,代入抛物线C1的方程,得y2-4my-4=0,
则y3+y4=4m,
∴x3+x4=my3+1+my4+1=4m2+2,
∴AC的中点坐标为E(2m2+1,2m),
由AC⊥BD,得BD的中点坐标为G(
+1,-
),
令2m2+1=
+1,得m2=1,此时2m2+1=
+1=3,
故直线过点H(3,0),
当m2≠1时,kHE=
=
,
同理kHG=
=
,
∴kHE=kHG,
∴E,H,G三点共线,
故直线过定点H(3,0).
设A(x1,y1),C(x2,y2),当直线AC的斜率为2时,
直线AC的方程为x=
| 1 |
| 2 |
代入抛物线C1的方程,得y2-2y-4=0,
设A(x1,y1),C(x2,y2),
则y1+y2=2,∴x1+x2=(
| 1 |
| 2 |
| 1 |
| 2 |
∴AC的中点坐标E(
| 3 |
| 2 |
由AC⊥BD,得直线BD的方程为x=-2y+1,
同理,得BD的中点坐标为G(9,-4),
由E(
| 3 |
| 2 |
(Ⅱ)直线EG过定点(3,0),设A(x3,y3),C(x4,y4),
直线AC的方程为x=my+1,代入抛物线C1的方程,得y2-4my-4=0,
则y3+y4=4m,
∴x3+x4=my3+1+my4+1=4m2+2,
∴AC的中点坐标为E(2m2+1,2m),
由AC⊥BD,得BD的中点坐标为G(
| 2 |
| m2 |
| 2 |
| m |
令2m2+1=
| 2 |
| m2 |
| 2 |
| m2 |
故直线过点H(3,0),
当m2≠1时,kHE=
| 2m-0 |
| 2m2+1-3 |
| m |
| m2-1 |
同理kHG=
-
| ||
|
| m |
| m2-1 |
∴kHE=kHG,
∴E,H,G三点共线,
故直线过定点H(3,0).
点评:本题考查直线方程的求法,考查直线是否过定点坐标的判断与求法,解题时要认真审题,注意中点坐标公式的合理运用.

练习册系列答案
相关题目
 如图,AB是圆O的直径,点C是圆O上异于A、B的点,直线PC⊥平面ABC,E,F分别为PA,PC的中点.
如图,AB是圆O的直径,点C是圆O上异于A、B的点,直线PC⊥平面ABC,E,F分别为PA,PC的中点. 如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.