题目内容
已知向量
=(x2,x+1),
=(1-x,t),若函数f(x)=
•
在区间(-1,1)上是增函数,则t的取值范围为 .
| a |
| b |
| a |
| b |
考点:平面向量数量积的运算,函数单调性的性质
专题:导数的概念及应用,平面向量及应用
分析:由数量积可得f(x),求导数可化问题为t≥3x2-2x在(-1,1)上恒成立,由二次函数的知识可得函数的值域,可得结论.
解答:
解:∵
=(x2,x+1),
=(1-x,t),
∴f(x)=
•
=x2(1-x)+t(x+1)=-x3+x2+tx+1,
∴f′(x)=-3x2+2x+t,
∵函数f(x)=
•
在区间(-1,1)上是增函数,
∴f′(x)=-3x2+2x+t≥0在(-1,1)上恒成立,
∴t≥3x2-2x在(-1,1)上恒成立,
而函数y=3x2-2x,x∈(-1,1)的值域为[-
,5)
∴t≥5
故答案为:t≥5
| a |
| b |
∴f(x)=
| a |
| b |
∴f′(x)=-3x2+2x+t,
∵函数f(x)=
| a |
| b |
∴f′(x)=-3x2+2x+t≥0在(-1,1)上恒成立,
∴t≥3x2-2x在(-1,1)上恒成立,
而函数y=3x2-2x,x∈(-1,1)的值域为[-
| 1 |
| 3 |
∴t≥5
故答案为:t≥5
点评:本题考查平面向量数量积和函数的单调性,涉及导数和恒成立问题,属中档题.

练习册系列答案
相关题目
若平面α∥平面β,直线a∥平面α,点B∈β,则在平面β内且过B点的所有直线中( )
| A、不一定存在与a平行的直线 |
| B、只有两条与a平行的直线 |
| C、存在无数条与a平行的直线 |
| D、存在唯一与a平行的直线 |
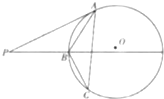 如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=
如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=