题目内容
已知函数f(x)=sin(2x-
),其中x∈(0,
),则f(x)的单调递减区间是 .
| π |
| 6 |
| π |
| 2 |
考点:复合三角函数的单调性
专题:三角函数的图像与性质
分析:由2kπ+
2x-
<2kπ+
可得函数所有的单调递减区间,找出满足x∈(0,
)的即可.
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 2 |
解答:
解:由2kπ+
2x-
<2kπ+
可解得kπ+
<x<kπ+
,
∴函数数f(x)=sin(2x-
)的单调递减区间为(kπ+
,kπ+
)k∈Z,
其中满足x∈(0,
)的为(
,
)
故答案为:(
,
)
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 3 |
| 5π |
| 6 |
∴函数数f(x)=sin(2x-
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
其中满足x∈(0,
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
故答案为:(
| π |
| 3 |
| π |
| 2 |
点评:本题考查三角函数的单调性,属基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
“a=1”是“函数f(x)=(x-1)2在区间[a,+∞)上为增函数”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E为AB的中点.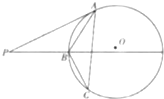 如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=
如图,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=9,C是圆上一点使得BC=4,∠BAC=∠APB,则AB=