题目内容
 我们把由半椭圆
我们把由半椭圆| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意可知c=
OF2求得c,再由OF2=
求得b,最后由a2=b2+c2求得a.
| 3 |
| b2-c2 |
解答:
解:∵OF2=
=
,OF0=c=
OF2=
,
∴b=1,
∴a2=b2+c2=1+
=
,
∴a=
,
∴ab=
,
故答案为:
| b2-c2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴b=1,
∴a2=b2+c2=1+
| 3 |
| 4 |
| 7 |
| 4 |
∴a=
| ||
| 2 |
∴ab=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题主要考查椭圆的性质,难度不大,熟练掌握椭圆的性质是解答的关键,属基础题.

练习册系列答案
相关题目
设圆柱的表面积为S,当圆柱体积最大时,圆柱的高为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、3π
|
函数f(x)=Asin(ωx+φ)+b的图象如图,则f(x)的解析式与S=f(0)+f(1)+f(2)+…+f(2010)的值分别为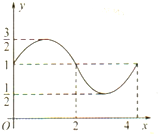 ( )
( )
 ( )
( )A、f(x)=
| ||||||
B、f(x)=sin
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
到两坐标轴距离相等的点的轨迹方程是( )
| A、y=x |
| B、x2-y2=0 |
| C、y=-x |
| D、y=|x| |
函数y=lnx+x的零点位于区间( )
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
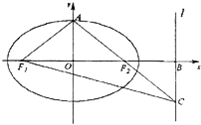 如图,椭圆
如图,椭圆