题目内容
不等式x-
>0成立的充分不必要条件是( )
| 1 |
| x |
| A、x>-1 |
| B、x>l |
| C、-l<x<0或x>l |
| D、x<-1或0<x<l |
考点:必要条件、充分条件与充要条件的判断
专题:不等式的解法及应用,简易逻辑
分析:求出不等式的解,根据充分不必要条件的定义进行求解即可.
解答:
解:由x-
>0得x>
,
若x>0,则x2>1,解得x>1,
若x<0,则x2<1,解得-1<x<0,
综上不等式x-
>0的等价条件是x>1或-1<x<0,
则x>1或-1<x<0的一个充分不必要条件可以是x>l,
故选:C.
| 1 |
| x |
| 1 |
| x |
若x>0,则x2>1,解得x>1,
若x<0,则x2<1,解得-1<x<0,
综上不等式x-
| 1 |
| x |
则x>1或-1<x<0的一个充分不必要条件可以是x>l,
故选:C.
点评:本题主要考查充分条件和必要条件的判断,求出不等式的等价条件是解决本题的关键.

练习册系列答案
相关题目
甲、乙两人从4门课程中各选修2门,则甲、乙两人所选的课程中有一门相同的选法有( )
| A、6种 | B、12种 |
| C、16种 | D、24 |
函数y=4sin(x+
)cos(x+
)是( )
| π |
| 2 |
| π |
| 2 |
| A、周期为2π的偶函数 |
| B、周期为2π的奇函数 |
| C、周期为π的偶函数 |
| D、周期为π的奇函数 |
已知函数f(x)=ex,对于曲线y=f(x)上横坐标城等差数列的三个点A、B、C,给出以下四个判断:①△ABC一定是钝角三角形;②△ABC可能是直角三角形;③△ABC可能是等腰三角形;④△ABC不可能是等腰三角形.其中正确的判断是( )
| A、①③ | B、①④ | C、②③ | D、②④ |
已知a>0,b>0,若不等式
+
≥
恒成立,则m的最大值等于( )
| 2 |
| a |
| 1 |
| b |
| m |
| 2a+b |
| A、7 | B、8 | C、9 | D、10 |
函数f(x)=loga(2x+3)+2(a>0,且a≠1)的图象恒过点( )
| A、(1,2) |
| B、(-1,2) |
| C、(1,3) |
| D、(-1,3) |
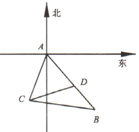 如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是
如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是