题目内容
已知双曲线C:
-
=1(a>0,b>0)的左右焦点分别为F1、F2,且F2恰为抛物线x=
y2的焦点,设双曲线C与该抛物线的一个交点为A,若△AF1F2是以AF1为底边的等腰三角形,则双曲线C的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:求出抛物线的焦点,可得c=1,即有双曲线的两焦点坐标,再由△AF1F2是以AF1为底边的等腰三角形,结合抛物线的定义,可得A(1,2),再由双曲线的定义可得a,由离心率公式计算即可得到.
解答:
解:抛物线x=
y2的焦点为(1,0),
即双曲线的c=1,F1(-1,0),F2(1,0),
可设A((m,n)(n>0),
则△AF1F2是以AF1为底边的等腰三角形,
则有AF2=F1F2=2c=2,
又抛物线的准线方程为x=-1,
由抛物线的定义可得AF2=m+1=2,
则m=1,n=2,A(1,2),
由双曲线的定义可得2a=AF1-AF2
=
-2,
即有a=
-1,
则离心率e=
=
=1+
.
故答案为:1+
.
| 1 |
| 4 |
即双曲线的c=1,F1(-1,0),F2(1,0),
可设A((m,n)(n>0),
则△AF1F2是以AF1为底边的等腰三角形,
则有AF2=F1F2=2c=2,
又抛物线的准线方程为x=-1,
由抛物线的定义可得AF2=m+1=2,
则m=1,n=2,A(1,2),
由双曲线的定义可得2a=AF1-AF2
=
| 22+22 |
即有a=
| 2 |
则离心率e=
| c |
| a |
| 1 | ||
|
| 2 |
故答案为:1+
| 2 |
点评:本题考查抛物线和双曲线的定义、方程和性质,考查运算能力,用好抛物线和双曲线的定义是解题的关键.

练习册系列答案
相关题目
已知双曲线
-
=1的右焦点到其渐近线的距离等于
,则该双曲线的离心率等于( )
| x2 |
| 4 |
| y2 |
| m2 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
半径为R的球内接一个正方体,则该正方体的体积是( )
A、
| ||||
B、
| ||||
C、2
| ||||
| D、8R3 |
不等式x-
>0成立的充分不必要条件是( )
| 1 |
| x |
| A、x>-1 |
| B、x>l |
| C、-l<x<0或x>l |
| D、x<-1或0<x<l |
在如下程序框图中,输入f0(x)=xex,若输出的fi(x)是(8+x)ex,则程序框图中的判断框应填入( )
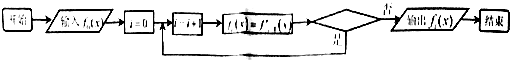
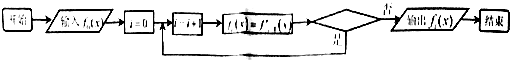
| A、i≤6 | B、i≤7 |
| C、i≤8 | D、i≤9 |