题目内容
已知a>0,b>0,若不等式
+
≥
恒成立,则m的最大值等于( )
| 2 |
| a |
| 1 |
| b |
| m |
| 2a+b |
| A、7 | B、8 | C、9 | D、10 |
考点:基本不等式
专题:不等式的解法及应用
分析:a>0,b>0,不等式
+
≥
恒成立,可得m≤[(2a+b)(
+
)]min,利用“乘1法”与基本不等式的性质即可得出.
| 2 |
| a |
| 1 |
| b |
| m |
| 2a+b |
| 2 |
| a |
| 1 |
| b |
解答:
解:∵a>0,b>0,不等式
+
≥
恒成立,
∴m≤[(2a+b)(
+
)]min,
∵(2a+b)(
+
)=5+
+
≥5+2×2
=9,当且仅当a=b=时取等号.
∴m的最大值等于9.
故选:C.
| 2 |
| a |
| 1 |
| b |
| m |
| 2a+b |
∴m≤[(2a+b)(
| 2 |
| a |
| 1 |
| b |
∵(2a+b)(
| 2 |
| a |
| 1 |
| b |
| 2b |
| a |
| 2a |
| b |
|
∴m的最大值等于9.
故选:C.
点评:本题考查了“乘1法”与基本不等式的性质、恒成立问题的等价转化方法,属于基础题.

练习册系列答案
相关题目
不等式x-
>0成立的充分不必要条件是( )
| 1 |
| x |
| A、x>-1 |
| B、x>l |
| C、-l<x<0或x>l |
| D、x<-1或0<x<l |
已知幂函数y=f(x)的图象过点(3,
),则f(9)=( )
| 3 |
| A、3 | ||
| B、-3 | ||
C、-
| ||
D、
|
在△ABC中,a,b,c分别为内角A,B,C的对边,已知a=5
,c=10,A=30°,则角B等于( )
| 2 |
| A、105° | B、60° |
| C、15° | D、105°或15° |
在如下程序框图中,输入f0(x)=xex,若输出的fi(x)是(8+x)ex,则程序框图中的判断框应填入( )
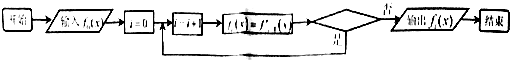
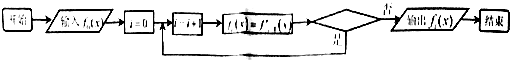
| A、i≤6 | B、i≤7 |
| C、i≤8 | D、i≤9 |