题目内容
5.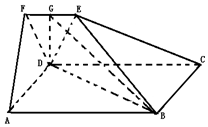 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.(Ⅰ)求证:DG⊥BC;
(Ⅱ)M是线段BD上一点,若GM∥平面ADF,求DM:MB的值.
分析 (Ⅰ)由已知可证DG⊥EF,又EF∥DC,可证DG⊥DC,由面面垂直证明DG⊥平面ABCD,即可证明DG⊥BC.
(Ⅱ)过M作MN∥AB交AD于N,连接FN,证明EG∥MN,GM∥FN,可得四边形FGMN是平行四边形,由已知可求$\frac{DM}{DB}=\frac{1}{6}$,进而可求$\frac{DM}{MB}=\frac{1}{5}$.
解答 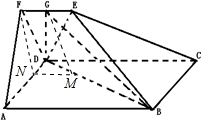 (本题满分为12分)
(本题满分为12分)
解:(Ⅰ)证明:∵DE=DF,G是EF的中点,
∴DG⊥EF,
又∵EF∥DC,
∴DG⊥DC,…(2分)
又∵平面ABCD⊥平面CDEF,平面ABCD∩平面CDEF=CD,
∴DG⊥平面ABCD,
又∵BC在平面ABCD内,
∴DG⊥BC.…(6分)
(Ⅱ)过M作MN∥AB交AD于N,连接FN,
∵EG∥DC,DC∥AB,
∴EG∥MN,
又∵GM∥平面ADF,
∴GM∥FN,
∴四边形FGMN是平行四边形,…(9分)
∴$MN=FG=\frac{1}{2}EF=\frac{1}{6}AB$,
∵$\frac{DM}{DB}=\frac{1}{6}$,
∴$\frac{DM}{MB}=\frac{1}{5}$.…(12分)
点评 本题考查了空间几何体的性质,空间直线的位置关系,直线平面的平行关系,考查了转化思想和数形结合思想,属于中档题.

练习册系列答案
相关题目
15.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的焦距为2c(c>0),以原点O为圆心,a为半径作圆,过点$(\frac{a^2}{c}\;,\;0)$作该圆的两条切线,若这两条切线互相垂直,则椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
16.甲、乙、丙、丁、戊五人排成一排,甲和乙都排在丙的同一侧,排法种数为( )
| A. | 12 | B. | 40 | C. | 60 | D. | 80 |
13.湖面上漂着一个小球,湖水结冰后将球取出,冰面上留下了一个半径为4cm,深2cm的空穴,则该球表面积为( ) cm2.
| A. | 400π | B. | 300π | C. | 200π | D. | 100π |
10.设a=log2$\frac{1}{3}$,b=($\frac{1}{2}$)3,c=3${\;}^{\frac{1}{2}}$,则( )
| A. | c<b<a | B. | a<b<c | C. | c<a<b | D. | b<a<c |
 ,
, ,函数
,函数 .求函数的最小正周期与最大值.
.求函数的最小正周期与最大值.