题目内容
15.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的焦距为2c(c>0),以原点O为圆心,a为半径作圆,过点$(\frac{a^2}{c}\;,\;0)$作该圆的两条切线,若这两条切线互相垂直,则椭圆的离心率为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
分析 先根据题意画出图形,如图,由切线PA、PB互相垂直,得出△OAP是等腰直角三角形,从而根据直角三角形的边的关系建立a,c之间的关系式,最后解得离心率即可.
解答  解:如图,切线PA、PB互相垂直,
解:如图,切线PA、PB互相垂直,
又半径OA垂直于PA,
∴△OAP是等腰直角三角形,
$\frac{{a}^{2}}{c}$=$\sqrt{2}$a.
解得:e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
则离心率e=$\frac{\sqrt{2}}{2}$,
故选A.
点评 本题考查椭圆的标准方程及简单几何性质,考查数形结合思想,属于中档题.

练习册系列答案
相关题目
5.计算 (1+i)(1-i)=( )
| A. | 2i | B. | 1-2i | C. | 2 | D. | 0 |
3.正四棱锥P-ABCD的侧棱长为$\sqrt{5}$,底面ABCD边长为2,E为AD的中点,则BD与PE所成角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
10.已知矩形ABCD中,AB=6,BC=4,E,F分别是AB,CD上两动点,且AE=DF,把四边形BCFE沿EF折起,使平面BCFE⊥平面ABCD,若折得的几何体的体积最大,则该几何体外接球的体积为( )
| A. | 28π | B. | $\frac{{28\sqrt{7}π}}{3}$ | C. | 32π | D. | $\frac{{64\sqrt{2}π}}{3}$ |
7.要得到y=cos2x-1的图象,只需将函数y=sin2x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位,再向上平移1个单位 | |
| B. | 向左平移$\frac{π}{4}$个单位,再向下平移1个单位 | |
| C. | 向右平移$\frac{π}{2}$个单位,再向上平移1个单位 | |
| D. | 向左平移$\frac{π}{2}$个单位,再向下平移1个单位 |
4.若圆(x-3)2+y2=1上只有一点到双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线的距离为1,则该双曲线离心率为( )
| A. | $\frac{{3\sqrt{5}}}{5}$ | B. | $\frac{{3\sqrt{3}}}{4}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
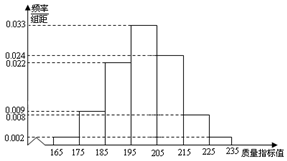 从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).
从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).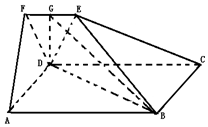 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.