题目内容
10.设a=log2$\frac{1}{3}$,b=($\frac{1}{2}$)3,c=3${\;}^{\frac{1}{2}}$,则( )| A. | c<b<a | B. | a<b<c | C. | c<a<b | D. | b<a<c |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:a=log2$\frac{1}{3}$<0,b=($\frac{1}{2}$)3∈(0,1),c=3${\;}^{\frac{1}{2}}$>1.
∴c>b>a.
故选:B.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
15.若区间[x1,x2]的 长 度 定 义 为|x2-x1|,函数f(x)=$\frac{({m}^{2}+m)x-1}{{m}^{2}x}$(m∈R,m≠0)的定义域和值域都是[a,b],则区间[a,b]的最大长度为( )
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 3 |
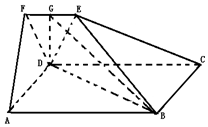 如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点.
如图,在五面体ABCDEF中,四边形ABCD为正方形,EF∥CD,平面CDFE⊥平面ABCD,且AD=3EF,DE=DF,点G为EF中点. ,
, ,且
,且 ,则m= ________;
,则m= ________;